Numerical Errors
Unexpected things can happen when you use floating point numbers!
Introduction
Sooner or later, you're going to want to include real, aka floating-point, numbers in your programs. Beit for measured quantities, or parameterisations, but integers don't always cut it. This is all fine and as it should be. A word of warning, however. Programs containing floating point numbers can do very odd things indeed! Use them with care.
A key reason why unexpected things happen is because you are sat in front of a digital computer, which is capable to storing and manipulating a finite number of discrete entities. This is contrasted against the infinite nature of real numbers. There are an infinity of real numbers between 0 and 1, say, or indeed between 0.000001 and 0.0000011. Also there is no theoretical limit to the number of digits in a decimal fraction.
Given the limited resources available to digital computers they must approximate the real line using a finite number of discrete points. It is this approximation which is the source of many of our surprises. Given the huge capacity of modern computers, it is easy to forget that this approximation exists. It's my goal in the sections below, to draw your attention to the areas in which ignoring this approximation will come back to bite you!
I didn't expect that! A tale of surprising Rounding Errors
Let's dive into our first example:
svn co https://svn.ggy.bris.ac.uk/subversion-open/numerics/trunk ./numerics cd numerics/examples/example1 make
There are two programs in this directory, one written in C, the other in Fortran. Let's run the C program first:
./surprising_c.exe
This program does some very simple arithmetic and yet we start to see odd things happening already! For example the trigonometric function tan can give us hugely different values depending upon whether we give it a single precision- (typically stored using 4 bytes) or a double precision- (8 byte) number. To be fair [math]\displaystyle{ \tan(\pi/2) }[/math] (radians) is undefined, and so it's hard to say what the right output should be. However, is does highlight that you need to be vigilant when using floating-point numbers and not to expect that your program's behaviour will always be predictable or benign.
Less dramatic, but perhaps more alarming is the next section of the program. This time, we take three double-precision numbers, initialise them to some values and then add them together. So simple, what could go wrong? Lots! it turns out..
xx (0.43) is: 0.42999999999999999334 yy (0.67) is: 0.67000000000000003997 zz (0.37) is: 0.36999999999999999556 xx + (yy + zz) is: 1.46999999999999997335 but.. (xx + yy) + zz is: 1.47000000000000019540
In this part of the program, we clearly see those approximations mentioned in the introduction. For example, we see that 0.43 is in fact stored as the approximation, 0.42999999999999999334. Then, when we accumulate other approximations made in the intermediate steps of the summation, we begin to understand that xx + (yy + zz) will indeed give us a different value to (xx + yy) + zz. Shocking! We definitely wouldn't want to write a test of the form:
if (total == 1.47) ...
The plain simplicity of these examples, coupled with their jarring results should warn us right away that there are many, many surprises waiting for us in programs involving floating-point numbers. Forewarned is forearmed.
Run the Fortran program (./surprising_f.exe) for completeness and note that while the tan function may be better behaved, floating-point arithmetic is still not associative, as a rule.
Truncation Errors
Roundoff errors aren't the only source of approximation in our programs, however. Consider solving a differential equation using the finite difference method. In case, it is common to approximate the value of a function using a truncated Taylor series. Discarding the higher order terms will introduce an error in our estimate of the function's value.
As an example, consider Euler's method for solving the Ordinary Differential Equation:
- [math]\displaystyle{ \frac{dy}{dt} = f(y,t) }[/math]
Using a forward difference, we approximate:
- [math]\displaystyle{ \frac{y^{j+1} - y^j}{\Delta t} = f(y^j,t^j) }[/math]
- [math]\displaystyle{ y^{j+1} = y^j + (\Delta t)f(y^j,t^j) }[/math]
It can be shown that the truncation error for each step of the solution is [math]\displaystyle{ O(\Delta t)^2 }[/math].
Total Error
For an iterative scheme, the truncation error per step is not the whole story, An estimate for [math]\displaystyle{ y^j }[/math] will inevitably depend upon the truncation errors accumulated over any previous steps. For the Euler method above, it can be shown that the total solution error due to cumulative truncation errors is [math]\displaystyle{ O(\Delta t) }[/math]. Euler's method is hence first order.
Other methods, such as a Runge-Kutta approach, may have different error characteristics.
Algorithms Matter: A Case of Catastrophic Cancellation
In this example, we're going to compare two iterative routines:
cd ../example2
The two formulations, derived from Archimedes' method of exhaustion, diverge in their approximations to [math]\displaystyle{ \pi }[/math].
For both, [math]\displaystyle{ \pi \approx 6 \times 2^i \times t_i }[/math], where
[math]\displaystyle{ t_0 = \frac{1}{\sqrt{3}} }[/math]
For the first method,
[math]\displaystyle{ t_{i+1} = \frac{\sqrt{{t_i}^2 + 1} - 1}{t_i} }[/math]
The second method has,
[math]\displaystyle{ t_{i+1} = \frac{t_i}{\sqrt{{t_i}^2 + 1} +1} }[/math]
which you can see is mathematically equivalent, but differs in a subtle and important way - the subtraction of 1 in the numerator.
All very interesting, you say, but a bit dry. Let's just run the example:
make ./pi.exe
We see the values for the first and second methods as the iterations tick by:
ii first method second method sqrt(t_i**2 + 1.0)
0 3.46410155296326 3.46410155296326
1 3.21539025919465 3.21539025919465 1.03527617933213
2 3.15965989465839 3.15965989465840 1.00862896032215
3 3.14608616830022 3.14608616830024 1.00214567074349
4 3.14271455296452 3.14271455296452 1.00053569932786
5 3.14187300333673 3.14187300333646 1.00013388000792
...
23 3.14000715793035 3.14159260695893 1.00000000000000
24 3.22451494240339 3.14159260695892 1.00000000000000
25 2.79111747371586 3.14159260695892 1.00000000000000
The second method converges nicely, but the first method loses the way. What went wrong? The problem lies in the value of [math]\displaystyle{ \sqrt{{t_i}^2 + 1} }[/math]. We see that this gets closer and closer to 1.
In the first method we subtract 1 from a number very close to 1. The result? We lose a whole bunch of significant digits and so we lose information and hence accuracy. Since the value of [math]\displaystyle{ t_i }[/math] is used to compute the value of [math]\displaystyle{ t_{i+1} }[/math] this loss of accuracy is propagated to the next iteration and so on and so forth. It is not surprising, then, that the calculation becomes very inaccurate and does not converge upon an approximation to [math]\displaystyle{ \pi }[/math].
By contrast, we preserve the significant digits in the second method, keep good accuracy and so converge.
Deterministic, yes. Identical outputs? no
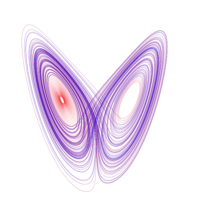
In this example, we will take a look at the Lorenz attractor. The equations which govern it:
- [math]\displaystyle{ \frac{dx}{dt} = \sigma (y - x) }[/math]
- [math]\displaystyle{ \frac{dy}{dt} = x (\rho - z) - y }[/math]
- [math]\displaystyle{ \frac{dz}{dt} = xy - \beta z }[/math]
are deterministic, but also embody mathematical chaos. [math]\displaystyle{ \sigma }[/math] is called the Prandtl number and [math]\displaystyle{ \rho }[/math] is called the Rayleigh number. For this example, we have set:
- [math]\displaystyle{ \sigma }[/math] = 10
- [math]\displaystyle{ \rho }[/math] = 28
- [math]\displaystyle{ \beta }[/math] = 8/3
Lorenz was interested in modelling the weather and introduced the equations as very simple atmospheric model. Thus we can see that even very simple models can be chaotic. This should act as a salutatory warning to us not to expect our models to produce the same outputs given a change of machine, compiler or even compiler options. Let's get the code, compile it and run it:
cd ../example3 make test
You will see that the makefile has created two executables. One was created using compiler options optimising for speed (lorenz-opt.exe), and the other was created without these optimisations (lorenz-noopt.exe). The test rule ran these two executables and collected the model output in appropriately named files. We can examine these outputs using the graphing package gnuplot:
gnuplot splot 'lorenz-noopt.dat' using 2:3:4 with lines replot 'lorenz-opt.dat' using 2:3:4 with lines
You will see that the two butterfly shaped tracks do not exactly align and so our two otherwise identical executables have produced different outputs given different compiler options. If we want to draw conclusions from our experiments, behaviour like this is definitely something we need to know about and the only way to find out about it, is to test our models.
An aside: We note that we had to push the gfortran compiler quite hard (switching on the -ffast-math optimisations) to give us different results, showing that the creators of gfortran have been careful in this regard. Not so if you use the ifort compiler. Even the default optimisations for speed are unsafe here and are enough to elicit different results.