NumMethodsPDEs
Numerical Methods for PDEs: Solving PDEs on a computer
Introduction
In this tutorial, we'll take a look at how we might model aspects of the world around us on a computer. When we use mathematics to describe many of the phenomena that we see we end up using Partial Differential Equations (PDEs), and so we seek ways to solve these numerically.
Looking at Nature (& a quick philosophical aside)
When we observe nature, certain patterns crop up again and again. For example, in the the field of electrostatics, if a function [math]\displaystyle{ f }[/math] describes a distribution of electric charge, then Poisson's equation:
- [math]\displaystyle{ {\nabla}^2 \varphi = f. }[/math]
gives the electric potential [math]\displaystyle{ \varphi }[/math].
However, Poisson's equation also describes the steady state temperature of a material when subjected to some heating and also crops up when considering gravitational potentials..
What's going on here? Why the recycling of the same equation? Is Poisson's equation fundamental in some way? Well, yes I suppose it is. However, we can look at it another way and say that Poisson's equation is the way we describe--using the language of maths--steady state phenomena which involve potentials. OK, this sounds a bit out there, but consider the following very general equation for a moment (it's a second-order linear equation in two variables):
[math]\displaystyle{ Au_{xx} + Bu_{xy} + Cu_{yy} + Du_x + Eu_y + Fu = G }[/math]
It turns out that we can categorise certain instances of this equation and then relate these categories to the kind of phenomena that they describe:
- Parabolic: [math]\displaystyle{ B^2 - 4AC = 0 }[/math]. This family of equations describe heat flow and diffusion processes.
- Hyperbolic: [math]\displaystyle{ B^2 - 4AC \gt 0 }[/math]. Describe vibrating systems and wave motion.
- Elliptic: [math]\displaystyle{ B^2 - 4AC \lt 0 }[/math]. Steady-state phenomena.
That's pretty handy!
The Finite Difference Method
In this section we'll look at solving PDEs using the Finite Difference Method. Finite difference equations have a long and illustrious past. Indeed, they were used by Newton and the gang as a logical route in to talk about differential calculus. So, in fact, we're just going to work back in the other direction..
Discritisation
The functions and variables that we see in, for instance, Poisson's equation are continuous; meaning that they could have an infinite number of values. This is fine when solving equations analytically, but we are limited to considering only a finite number of values when solving PDEs with digital computer. We need a way to discritise our problems. Happily, help is at hand from the Taylor series. Recall that we can approximate the value of a function at a point distant (displaced by an amount h) from x using a linear summation of derivatives of the function at x:
- [math]\displaystyle{ f(x+h) \approx f(x) + \frac{f'(x)}{1!}h + \frac{f''(x)}{2!}h^2 + \cdots }[/math]
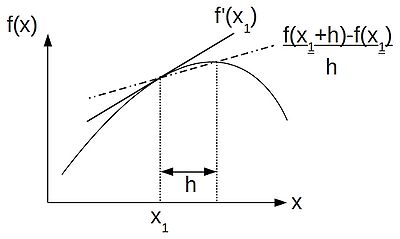
Let's truncate this series after the first differential and rearrange, to get ourselves the forward-difference approximation:
- [math]\displaystyle{ f'(x) \approx \frac{f(x+h) - f(x)}{h} }[/math]
Thus, following the finite difference approach, we can discritise our equations by replacing our differential operators by their difference approximations, as helpfully provided by a truncated Taylor series. If, like me, you like thinking visually, the schematic below shows the relationship between a differential operator--the gradient at a point [math]\displaystyle{ x_1 }[/math] and the finite difference approximation to the gradient:
If we were to consider a displacement of -h instead, we would get the backward-difference approximation to [math]\displaystyle{ f'(x) }[/math]:
- [math]\displaystyle{ f'(x) \approx \frac{f(x) - f(x-h)}{h} }[/math],
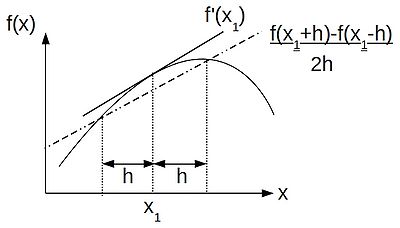
Subtracting the backward from the forward we can generate the central-difference approximation:
- [math]\displaystyle{ f'(x) \approx \frac{1}{2h}(f(x+h) - f(x-h)) }[/math].
By retaining an extra term from the Taylor series, and some similar rearrangements, we can also formulate a finite difference approximation to the 2nd differential. For example the central-difference formula for this is:
- [math]\displaystyle{ f''(x) \approx \frac{1}{h^2} [ f(x+h) - 2f(x) + f(x-h) ] }[/math].
In a similar way we can derive formulae for approximations to partial derivatives. Armed with all these formulae, we can convert differential equations into difference equations, which we can solve on a computer. Since we are dealing with approximations to the original equation(s), we must be vigilant that errors in our input and intermediate calculations do not accumulate such that our final solution is meaningless.
Eliptical Equations: Discrete Laplacian Operator
Consider Laplace's equation in 2-dimensions:
- [math]\displaystyle{ \frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2} = 0 }[/math]
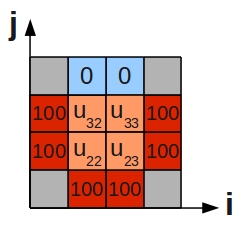
This describes purely diffusive phenomena and can give us the steady state temperature over a 2D plate, three sides of which are held at 100°C, while the fourth is held at 0°C. We have divided the plate into a number of grid cells:
Using the central difference approximation to a 2nd differential that we derived in the last section, we can rewrite the differential equation as a difference equation:
- [math]\displaystyle{ \frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2} \approx \frac{1}{h^2}(u^j_{i+1} -2u^j_i +u^j_{i-1}) + \frac{1}{k^2}(u^{j+1}_i -2u^j_i +u^{j-1}_i) }[/math]
where h is the grid spacing in the i-directions and k is the spacing the j-direction. If we set [math]\displaystyle{ h=k }[/math], then:
- [math]\displaystyle{ u^j_{i+1} + u^j_{i-1} + u^{j+1}_i + u^{j-1}_i - 4u^j_i = 0 }[/math]
solving for [math]\displaystyle{ u^j_i }[/math]:
- [math]\displaystyle{ u^j_i = \frac{1}{4}(u^j_{i+1} + u^j_{i-1} + u^{j+1}_i + u^{j-1}_i) }[/math]
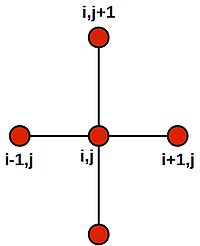
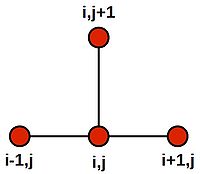
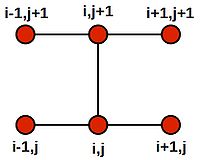
Note that this last equation says--quite intuitively--that the value at the central grid point is equal to the average of its four neighbours. We can draw a picture of the stencil needed to compute the value:
Placing the stencil on the 4 grid cells on the inner region (orange) in turn, we generate the following 4 difference equations:
- [math]\displaystyle{ \begin{alignat}{5} -4u_{22} & + u_{32} & + u_{23} & + 100 & + 100 & = 0 \\ -4u_{32} & + 0 & + u_{33} & + u_{22} & + 100 & = 0 \\ -4u_{23} & + u_{33} & + 100 & + 100 & + u_{22} & = 0 \\ -4u_{33} & + 0 & + 100 & + u_{23} & + u_{32} & = 0 \\ \end{alignat} }[/math]
This system of equations can be written in matrix form:
- [math]\displaystyle{ \begin{bmatrix}-4 & 1 & 1 & 0\\1 & -4 & 0 & 1\\1 & 0 & -4 & 1\\0 & 1 & 1 & -4\end{bmatrix} \begin{bmatrix}u_{22}\\u_{32}\\u_{23}\\u_{33}\end{bmatrix} = \begin{bmatrix}-200\\-100\\-200\\-100\end{bmatrix} }[/math]
Which may be summarised as the vector equation, Ax=b, which can be efficiently & conveniently solved using a library linear algebra routines, such as LAPACK, PETSc or PLASMA.
Parabolic Equations: Forward (Explicit) Euler
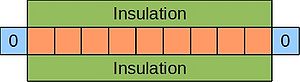
One example of a parabolic equation is the 1D heat equation, which describes the evolution of temperature at various points in a thin, insulated bar over time. Imagine such a bar where the ends are kept at 0°C:
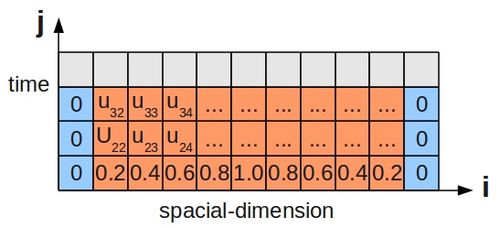
Since this scenario involves the passage of time, just stating the boundary conditions is not enough, and we must also specify some initial condition for the temperature along the bar's length. This is shown below for a bar divided up into grid cells, as before:
The 1D heat equation is:
- [math]\displaystyle{ \frac{\partial u}{\partial t}=\alpha \frac{\partial^2u}{\partial x^2} }[/math]
where [math]\displaystyle{ \alpha }[/math]--the thermal diffusivity--is set to 1 for simplicity. One way to rewrite this as a difference equation (using a forward difference for the LHS and a central difference for the RHS) is:
- [math]\displaystyle{ \frac{u^{j+1}_i - u^j_i }{k} = \frac{u^j_{i+1} - 2u^j_i + u^j_{i-1}}{h^2} }[/math]
and rearrange to solve for [math]\displaystyle{ u^{j+1}_i }[/math]:
- [math]\displaystyle{ u^{j+1}_i = u^j_i + r(u^j_{i+1} - 2u^j_i + u^j_{i-1}) }[/math]
- [math]\displaystyle{ u^{j+1}_i = ru^j_{i+1} + (1- 2r)u^j_i + ru^j_{i-1} }[/math]
where:
[math]\displaystyle{ r=\frac{k}{h^2} }[/math]
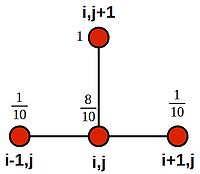
This time, we see that the appropriate stencil is:
If we set [math]\displaystyle{ h=\frac{1}{10} }[/math] and [math]\displaystyle{ k=\frac{1}{1000} }[/math], then [math]\displaystyle{ r=\frac{1}{10} }[/math], and the equation becomes:
- [math]\displaystyle{ u^{j+1}_i = u^j_i + \frac{1}{10}(u^j_{i+1} - 2u^j_i + u^j_{i-1}) }[/math]
- [math]\displaystyle{ u^{j+1}_i = \frac{1}{10}(u^j_{i+1} + 10u^j_i - 2u^j_i + u^j_{i-1}) }[/math]
- [math]\displaystyle{ u^{j+1}_i = \frac{1}{10}(u^j_{i+1} + 8u^j_i + u^j_{i-1}) }[/math]
Which we can illustrate using weightings on the stencil nodes:
Forward Euler is as an explicit method, as one unknown value ([math]\displaystyle{ u^{j+1}_i }[/math]) is expressed directly in terms of known values (all values of u at time j are known).
We could implement a simple marching algorithm, where we centre the stencil over a set of known values at time j, and may calculate the unknown temperature for grid cell i at time j+1. However, it would be better to group together all the calculations for a particular time step into a system of simultaneous equations (for our example 1d heat problem):
- [math]\displaystyle{ u_{22} = \frac{1}{10}(0) + \frac{8}{10}(0.2) + \frac{1}{10}(0.4) }[/math]
- [math]\displaystyle{ u_{23} = \frac{1}{10}(0.2) + \frac{8}{10}(0.4) + \frac{1}{10}(0.6) }[/math]
- [math]\displaystyle{ u_{24} = \frac{1}{10}(0.4) + \frac{8}{10}(0.6) + \frac{1}{10}(0.8) }[/math]
- [math]\displaystyle{ \cdots }[/math]
and then re-write in matrix form:
- [math]\displaystyle{ \begin{bmatrix}u_{22} \\ u_{23} \\ u_{24} \\\vdots \end{bmatrix} = \begin{bmatrix} 0.1 & 0.8 & 0.1 & 0 & 0 & \cdots & 0 \\ 0 & 0.1 & 0.8 & 0.1 & 0 & \cdots & 0 \\ \vdots & & & & & & \vdots \\ & & \cdots & 0 & 0.1 & 0.8 & 0.1 \\ \end{bmatrix} \times \begin{bmatrix}0 \\ 0.2 \\ 0.4 \\ \vdots \\ 0.2 \\ 0 \end{bmatrix} }[/math]
as the computational efficiency of a matrix vector multiplication will be hard to better. Note that we can write the above piece of linear algebra in a general form:
- [math]\displaystyle{ \begin{bmatrix}u_{22} \\ u_{23} \\ u_{24} \\ \vdots \end{bmatrix} = \begin{bmatrix} r & 1-2r & r & 0 & 0 & \cdots & 0 \\ 0 & r & 1-2r & r & 0 & \cdots & 0 \\ \vdots & & & & & & \vdots \\ & & \cdots & 0 & r & 1-2r & r \\ \end{bmatrix} \times \begin{bmatrix}u_{11} \\ u_{12} \\ u_{13} \\ u_{14} \\ \vdots \end{bmatrix} }[/math]
Solution Stability and the CFL Condition
The Forward Euler scheme has the benefit of simplicity, but is unstable for large time steps. The CFL (Courant–Friedrichs–Lewy) condition states that the following must hold:
- [math]\displaystyle{ r=\frac{k}{h^2} \le 0.5 }[/math]
for stability.
Parabolic Equations: Backward (Implicit) Euler
An alternative way to formulate our finite difference is to use a backward-difference. The backward Euler scheme requires more computation per time-step than the forward scheme, but has the distinct advantage that it is unconditionally stable with regard to the relative size between the spatial and time step sizes; i.e. we are not limited to [math]\displaystyle{ r \le 0.5 }[/math] when we use the backward Euler scheme.
We will use a central-difference on the RHS, as before, but shifting the time index to [math]\displaystyle{ j+1 }[/math]. This will allow us to formulate a backward-difference on the RHS between the time indices [math]\displaystyle{ j }[/math] and [math]\displaystyle{ j+1 }[/math]:
- [math]\displaystyle{ \frac{u^{j+1}_i - u^j_i }{k} = \frac{u^{j+1}_{i+1} - 2u^{j+1}_i + u^{j+1}_{i-1}}{h^2} }[/math]
- [math]\displaystyle{ u^{j+1}_i - u^j_i = \frac{k}{h^2}(u^{j+1}_{i+1} - 2u^{j+1}_i + u^{j+1}_{i-1}) }[/math]
- [math]\displaystyle{ u^{j+1}_i - u^j_i = r(u^{j+1}_{i+1} - 2u^{j+1}_i + u^{j+1}_{i-1}) }[/math]
- [math]\displaystyle{ u^{j+1}_i - u^j_i = ru^{j+1}_{i+1} - 2ru^{j+1}_i + ru^{j+1}_{i-1} }[/math]
- [math]\displaystyle{ u^{j+1}_i - ru^{j+1}_{i+1} + 2ru^{j+1}_i - ru^{j+1}_{i-1} = u^j_i }[/math]
- [math]\displaystyle{ u^j_i = - ru^{j+1}_{i+1} + (1 + 2r)u^{j+1}_i - ru^{j+1}_{i-1} }[/math]
If we again choose [math]\displaystyle{ h=\frac{1}{10} }[/math] and [math]\displaystyle{ k=\frac{1}{1000} }[/math], such that [math]\displaystyle{ r=\frac{k}{h^2}=\frac{1}{10} }[/math], as before, we end up with the following system of equations when we consider all values of [math]\displaystyle{ i }[/math] for our first time-step--from [math]\displaystyle{ j }[/math] to [math]\displaystyle{ j+1 }[/math]--where we know values of all the cells at time [math]\displaystyle{ j }[/math]:
- [math]\displaystyle{ 0.2 = -\frac{1}{10}(0) + \frac{12}{10}(u_{22}) -\frac{1}{10}(u_{23}) }[/math]
- [math]\displaystyle{ 0.4 = -\frac{1}{10}(u_{22}) + \frac{12}{10}(u_{23}) -\frac{1}{10}(u_{24}) }[/math]
- [math]\displaystyle{ 0.6 = -\frac{1}{10}(u_{23}) + \frac{12}{10}(u_{24}) -\frac{1}{10}(u_{25}) }[/math]
- [math]\displaystyle{ \cdots }[/math]
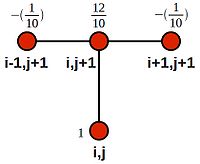
We can see that this is akin to looping over the domain with the following stencil:
Rearranging, so that we have only constants on the RHS:
- [math]\displaystyle{ \frac{1}{10}(0) + \frac{12}{10}(u_{22}) -\frac{1}{10}(u_{23}) = 0.2 + \frac{1}{10}(0) }[/math]
- [math]\displaystyle{ \frac{1}{10}(u_{22}) + \frac{12}{10}(u_{23}) -\frac{1}{10}(u_{24}) = 0.4 }[/math]
- [math]\displaystyle{ \frac{1}{10}(u_{23}) + \frac{12}{10}(u_{24}) -\frac{1}{10}(u_{25}) = 0.6 }[/math]
- [math]\displaystyle{ \cdots }[/math]
We can re-write this system of equations in matrix form:
- [math]\displaystyle{ \begin{bmatrix} 1.2 & -0.1 & 0 & 0 & \cdots & 0 \\ -0.1 & 1.2 & -0.1 & 0 & \cdots & 0 \\ \vdots & & & & & \vdots \\ & & \cdots & 0 & -0.1 & 1.2 \\ \end{bmatrix} \times \begin{bmatrix} u_{22} \\ u_{23} \\ u_{24} \\\vdots \end{bmatrix} = \begin{bmatrix} 0.2 + 0.1(0) \\ 0.4 \\ \vdots \\ 0.2 +0.1(0) \end{bmatrix} }[/math]
The general form is:
- [math]\displaystyle{ \begin{bmatrix} 1+2r & -r & 0 & 0 & \cdots & 0 \\ -r & 1+2r & -r & 0 & \cdots & 0 \\ \vdots & & & & & \vdots \\ & & \cdots & 0 & -r & 1+2r \\ \end{bmatrix} \times \begin{bmatrix} u_{22} \\ u_{23} \\ u_{24} \\\vdots \end{bmatrix} = \begin{bmatrix} u_{12} + r(u_{11}) \\ u_{13} \\ \vdots \\ u_{1n-1} + r(u_{1n}) \end{bmatrix} }[/math]
Parabolic Equations: Crank-Nicolson
A third scheme for solving the 1D heat equation is to create a finite difference equation using the Crank-Nicolson stencil:
The stencil amounts to an average of both the forward and backward Euler methods. The resulting difference equation is:
- [math]\displaystyle{ \frac{u^{j+1}_i - u^j_i}{k} = \frac{1}{2}(\frac{u^{j+1}_{i+1} - 2u^{j+1}_{i} + u^{j+1}_{i-1}}{h^2} + \frac{u^j_{i+1} - 2u^j_i + u^j_{i-1}}{h^2}). }[/math]
Which we may rearrange to become:
- [math]\displaystyle{ u^{j+1}_i - u^j_i = \frac{1}{2}\frac{k}{h^2}(u^{j+1}_{i+1} - 2u^{j+1}_i + u^{j+1}_{i-1} + u^j_{i+1} - 2u^j_i + u^j_{i-1}) }[/math]
- [math]\displaystyle{ 2(u^{j+1}_i - u^j_i) = r(u^{j+1}_{i+1} - 2u^{j+1}_i + u^{j+1}_{i-1} + u^j_{i+1} - 2u^j_i + u^j_{i-1}) }[/math],
where [math]\displaystyle{ r=\frac{k}{h^2} }[/math].
Collecting the unknowns (values of u at the next timestep, [math]\displaystyle{ j+1 }[/math]) to the LHS and the knowns (values of u at current timestep, [math]\displaystyle{ j }[/math]), we get:
- [math]\displaystyle{ 2u^{j+1}_i + 2ru^{j+1}_i - ru^{j+1}_{i+1} - ru^{j+1}_{i-1} = 2u^j_i +ru^j_{i+1} -2ru^j_i + ru^j_{i-1} }[/math]
- [math]\displaystyle{ (2+2r)u^{j+1}_i - ru^{j+1}_{i+1} - ru^{j+1}_{i-1} = (2-2r)u^j_i +ru^j_{i+1} + ru^j_{i-1} }[/math].
If we choose [math]\displaystyle{ h=1/10 }[/math] and [math]\displaystyle{ k=1/100 }[/math] (note that the time-step is 10x larger than than chosen for the forward Euler example), then [math]\displaystyle{ r=1 }[/math], and we get:
- [math]\displaystyle{ -u_{i-1}^{j+1} +4u_i^{j+1} -u_{i+1}^{j+1} = u_{i-1}^j + u_{i+1}^j }[/math].
We can again create a system of linear equations for all the cells j along the bar at a given time step i:
- [math]\displaystyle{ -0 + 4u_{22} - u_{23} = 0 + 0.4 }[/math]
- [math]\displaystyle{ -u_{22} + 4u_{23} - u_{24} = 0.2 + 0.6 }[/math]
- [math]\displaystyle{ -u_{23} + 4u_{24} - u_{25} = 0.4 + 0.8 }[/math]
- [math]\displaystyle{ \cdots }[/math]
We have [math]\displaystyle{ j }[/math] unknowns and [math]\displaystyle{ j }[/math] equations. Then we can again translate into matrix notation and solve using a library linear algebra routines:
- [math]\displaystyle{ \begin{bmatrix} -4 & 1 & 0 & 1 & 0 & 0 & \cdots & 0 \\ 1 & -4 & 1 & 0 & 1 & 0 & \cdots & 0 \\ \vdots & & & & & & & \vdots \\ & \cdots & & 0 & 1 & 0 & 1 & -4\\ \end{bmatrix} \times \begin{bmatrix} u_{22} \\ u_{23} \\ u_{24} \\\vdots \end{bmatrix} = \begin{bmatrix} 0 + 0.4 \\ 0.2 + 0.6 \\ \vdots \\ 0 + 0.4 \end{bmatrix} }[/math]
In general:
- [math]\displaystyle{ \begin{bmatrix} -(2+2r) & r & 0 & r & 0 & 0 & \cdots & 0 \\ r & -(2+2r) & r & 0 & r & 0 & \cdots & 0 \\ \vdots & & & & & & & \vdots \\ & \cdots & & 0 & r & 0 & r & -(2+2r)\\ \end{bmatrix} \times \begin{bmatrix} u_{22} \\ u_{23} \\ u_{24} \\\vdots \end{bmatrix} = \begin{bmatrix} ru_{11} + (2-2r)u_{12} + ru_{13} \\ \vdots \end{bmatrix} }[/math]
Other Numerical Methods
We have looked at the finite difference method (FDM) here, but other (more mathsy) approaches exist, such as the finite element and finite volume methods. Each approach has its pros and cons. For example, the FDM is limited to regular grids spread over rectangular domains, but is easy to program. In contrast the FEM is applicable to intricately shaped domains and the resolution of the individual elements can be varied, but is requires more involved programming and a deeper level of understand of the relevant mathematics. However, one thing is common to all the approaches--the problem boils down to a system of linear equations to solve, and that a library of linear algebra routines will be the workhorse when finding solutions to PDEs on a computer. Repeat after me, "a fast linear algebra library is key!"
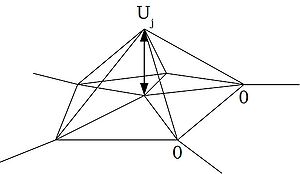
The Finite Element Method (FEM)
The general approach here is to create a potential function from our PDE and to find a solution to it via minimising the potential function. Key steps include:
- Discritisation of the original PDE, often by proposing that we can approximate the solution using a linear sum of (polynomial) basis functions.
- Create the potential function by invoking the method of weighted residuals, and in particular the Galerkin specialisation of this approach.
- Use whatever algebraic manipulation and integration (possibly numerical) is required to create a system of linear equations.
- Solve said system and in doing so, solve the original PDE.
Consider, for example, Poisson's equation over a 2-dimensional region, [math]\displaystyle{ R }[/math]:
- [math]\displaystyle{ \nabla^2u=f(x,y) }[/math]
where [math]\displaystyle{ u=0 }[/math] at the boundary of the domain.
Following the method of weighted residuals, we multiply both sides by test/basis functions [math]\displaystyle{ \phi_i }[/math], and take integrals over the domain:
- [math]\displaystyle{ \iint\limits_R \nabla^2u\phi_i\, dA = \iint\limits_R f\phi_i\, dA }[/math]
Recall integration by parts, for two arbitrary functions, [math]\displaystyle{ g(x) }[/math] and [math]\displaystyle{ h(x) }[/math]:
- [math]\displaystyle{ \int g(x)h'(x)\, dx = g(x)h(x) - \int g'(x)h(x)\, dx }[/math]
- [math]\displaystyle{ g(x)h'(x)\, dx = \nabla g(x)h(x) - g'(x)h(x)\, dx }[/math]
Applying integration by parts to [math]\displaystyle{ \nabla^2u\phi_i }[/math] we get:
The divergence of a vector field [math]\displaystyle{ F }[/math] is [math]\displaystyle{ div F = \nabla \cdot F }[/math]. Gauss' Divergence Theorem states, for the region [math]\displaystyle{ R }[/math] bounded by s:
- [math]\displaystyle{ \iint\limits_R \nabla \cdot F\, dA = \oint\limits_s F \cdot n\, ds }[/math]
where [math]\displaystyle{ n }[/math] is the unit vector normal to the surface.
FEM packages include: