NumericPython
numpy: An intro to some handy array tools in Python
A Quick Introduction to Python
Python is a high-level scripting language than can prove useful in a number of situations. On this page, we will mostly be looking at the array processing functions available through it's numpy package. However, we'll start with a little taster of the core language by way of an introduction. Python has lots to offer to the scientific programmer, through the routines contained within it's Scientific and numpy packages (offering a possible alternative to Matlab, IDL or R, for example), as well as it's visualisation tools. Python can also act as a flexible front-end to your Fortran or C routines. If you would like a more complete introduction to the language, there are a number of very good online tutorials (such as [1], for example), and also some good books by O'Reilly and New Riders, to name a couple. Python is freely available (and by that I mean gratis, at no cost) for Linux, Mac and Windows.
Getting Started with an Interactive Session
You can write scripts or start up the Python interpreter for an interactive session. We'll make a start interactively and move on to writing scripts later. At the Linux command line, you can invoke the interpreter by just typing:
python
and you should see something similar to:
Python 2.4.3 (#1, Jan 21 2009, 01:11:33) [GCC 4.1.2 20071124 (Red Hat 4.1.2-42)] on linux2 Type "help", "copyright", "credits" or "license" for more information. >>>
where we can type at the >>> prompt. To exit the interpreter, type Ctrl-D (i.e. the control key and D. Lower case is fine.)
OK, great! We're out of the starting gate. Let's get into our stride.
First, let's set a variable to a message. For example:
>>> message = "Hello, Gethin!"
Then type:
>>> print message
and, gratifyingly , I get:
hello, Gethin!
Python can, of course, do arithmetic, logic and all that good stuff. Just as an example, you could try some of the following:
>>> print 39 + 1
>>> print 2.2 * 3.3
>>> pi = 22/7 >>> print pi
>>> pi = 22.0/7.0 >>> print pi
>>> a=a=1.5+0.5j >>> print a.real ... >>> print a.imag
>>> if len(message) > 10: ... print "message has more than 10 characters" ...
You'll have to throw in a tab and hit enter a couple of times for the last one. And notice the good-old integer division gotcha in the approximation of pi.
Some Higher-Level Features
In the preamble, we mentioned that Python is a high-level language. What does that mean, exactly? Well, Python has some rather powerful data-types, such as lists and hash-tables aka 'dictionaries' built in, and also provides a rich language for manipulating the data-types that you are used to seeing in lower-level languages such as C and Fortran.
For example, the eagle-eyed will have spotted in the previous examples that we could ask the length a character string--straight off the bat. No need to write a counting routine ourselves:
>>> print len(message)
We also take slices of our character string. In my case
>>> print message[:5]
elicits:
hello
An example of a list is:
>>> shopping = ['bread', 'marmalade', 'milk', 'tea']
and we can enquire about the length of that using the same function as before:
>>> len(shopping)
We can also take slices of a list, as we did with a string:
>>> shopping[0:2]
and even reset a portion of the list that way:
>>> shopping[0:2] = ['bagels', 'jam'] >>> shopping
A list object comes with a number of handy methods built in. For example we could type:
>>> shopping.append("butter")
>>> print shopping
and even:
>>> shopping.reverse() >>> print shopping
or
>>> shopping.sort() >>> print shopping
Arrays in numpy
OK, we could spend quite a while getting to grips with all of Python's myriad features, but we'll move onto looking at numerical features and arrays in particular. To do this we will load a package. You can do this by typing:
from numpy import *
Now that we have access to the package, let's create an array. Note that a numpy array is an objects of a different type to an intrinsic array in Python. A simple approach is to use the array function. For example we might enter:
>>> a = array([[1.0, 0.0, 0.0],[0.0, 1.0, 0.0],[0.0, 0.0, 1.0]]) >>> print a
Given an array, we may enquire about it's shape:
>>> print a.shape
and we are told that it is a 2-dimensional array (i.e. an array of rank 2) and that the length of both dimensions is 3:
(3, 3)
Should we so desire, we could re-shape the array. One way to do this is to to set it's shape attribute directly:
>>> a.shape = (1,9) >>> print a
We can also apply operators to array objects. For example:
>>> a = a * 9 >>> print a
Note, however, that most operations on numpy arrays are done element-wise, which may be different to a linear algera operation that you were expecting. We will return to linear algebra operations in a later section.
As with the list example, it can be useful to read or change the value of an element (or sub array) indidually. Let's turn the array back to it's rank-2 form and try it out:
>>> a.shape = (3,3) >>> a[1,1] = 777.0 >>> print a >>> a[1:,1:] = [[777.0, 777.0],[777.0, 777.0]] >>> print a
This is all pretty handy so far, but specifying the value of each element explicitly could become a chore. Happily some helper functions exist to give you a head start with some building blocks. For example, your can use:
>>> b = zeros((3,3) >>> print b >>> b = ones((3,2)) >>> print b >>> b = identity(2) >>> print b >>> big = resize(b, (6,6)) >>> print big
The use of resize in the last example illustrates a useful replicating feature.
Visualising the Contents of an Array
The above examples are quite natty, but we have deliberately kept the array sizes small so that we can print the element values easily. In practice, you may find that your array sizes are much larger and printing the values to the screen is impractical. Fear not! Python has many packages which help you plot your data, so that you can explore it. One of the many possibilities are outlines below, where we have crafted an array of values which are more pleasing to the eye thusly:
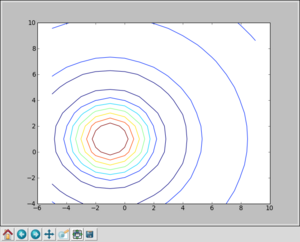
>>> x = arange(-5,10) >>> y = arange(-4,11) >>> z1 = sqrt(add.outer(x**2,y**2)) >>> Z = sin(z1)/z1 >>> import matplotlib.pyplot as plt >>> from pylab import meshgrid >>> X, Y = meshgrid(x,y) >>> plt.figure() >>> plt.contour(X,Y,Z) >>> plt.show()
and you should get a window similar to:
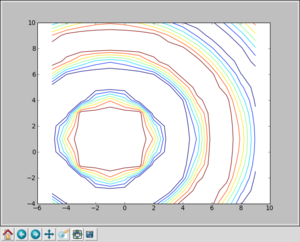
The clip function is an interesting one. Using it, we can replace values greater than some threshold with a ceiling and lower than another threshold with a floor. For example:
>>> Z1 = clip(Z,-0.1,0.1) >>> plt.figure() >>> plt.contour(X,Y,Z1) >>> plt.show()
gives us: