NumMethodsPDEs
Numerical Methods for PDEs: Solving PDEs on a computer
Introduction
In this tutorial, we'll take a look at how we might model aspects of the world around us on a computer. When we use mathematics to describe many of the phenomena that we see we end up using Partial Differential Equations (PDEs), and so we seek ways to solve these numerically.
Looking at Nature (& a quick philosophical aside)
When we observe nature, certain patterns crop up again and again. For example, in the the field of electrostatics, if a function [math]\displaystyle{ f }[/math] describes a distribution of electric charge, then Poisson's equation:
- [math]\displaystyle{ {\nabla}^2 \varphi = f. }[/math]
gives the electric potential [math]\displaystyle{ \varphi }[/math].
However, Poisson's equation also describes the steady state temperature of a material when subjected to some heating and also crops up when considering gravitational potentials..
What's going on here? Why the recycling of the same equation? Is Poisson's equation fundamental in some way? Well, yes I suppose it is. However, we can look at it another way and say that Poisson's equation is the way we describe--using the language of maths--steady state phenomena which involve potentials. OK, this sounds a bit out there, but consider the following very general equation for a moment (it's a second-order linear equation in two variables):
[math]\displaystyle{ Au_{xx} + Bu_{xy} + Cu_{yy} + Du_x + Eu_y + Fu = G }[/math]
It turns out that we can categorise certain instances of this equation and then relate these categories to the kind of phenomena that they describe:
- Parabolic: [math]\displaystyle{ B^2 - 4AC = 0 }[/math]. This family of equations describe heat flow and diffusion processes.
- Hyperbolic: [math]\displaystyle{ B^2 - 4AC \gt 0 }[/math]. Describe vibrating systems and wave motion.
- Elliptic: [math]\displaystyle{ B^2 - 4AC \lt 0 }[/math]. Steady-state phenomena.
That's pretty handy!
Discritisation
OK, so far so good. However, the functions and variables that we've considered thus far are continuous, meaning that they could have an infinite number of values. This is fine when solving equations analytically, but we need to deal with a finite number of values when working with a digital computer. We need a way to discritise our problems. Happily, help is at hand from the Taylor series. Recall that we can approximate the value of a function at a point distant (displaced by an amount h) from x using a linear summation of derivatives of the function at x:
- [math]\displaystyle{ f(x+h) \approx f(x) + \frac{f'(x)}{1!}h + \frac{f''(x)}{2!}h^2 + \cdots }[/math]
Let's truncate this series after the first differential and rearrange:
- [math]\displaystyle{ f'(x) \approx \frac{f(x+h) - f(x)}{h} }[/math]
This is called the forward-difference approximation to the first derivative, [math]\displaystyle{ f'(x) }[/math]. If we were to consider a displacement of -h, we would end up with:
- [math]\displaystyle{ f'(x) \approx \frac{f(x) - f(x-h)}{h} }[/math],
which is called the backward-difference. Subtracting the backward from the forward we can generate:
- [math]\displaystyle{ f'(x) \approx \frac{1}{2h}(f(x+h) - f(x-h)) }[/math],
the central-difference approximation.
By retaining an extra term from the Taylor series, and some similar rearrangements, we can also formulate a finite difference approximation to the 2nd differential. For example the 'central-difference formula is:
- [math]\displaystyle{ f''(x) \approx \frac{1}{h^2}(f(x+h) - 2f(x) + f(x-h)) }[/math]
Armed with these formulae, we can convert differential equations into difference equations, which we can solve on a computer.
Eliptical Equations: Discrete Laplacian Operator
Consider Laplace's equation in 2-dimensions:
- [math]\displaystyle{ \frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2} = 0 }[/math]
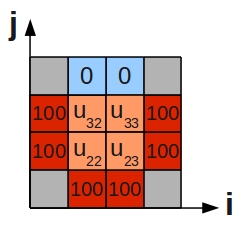
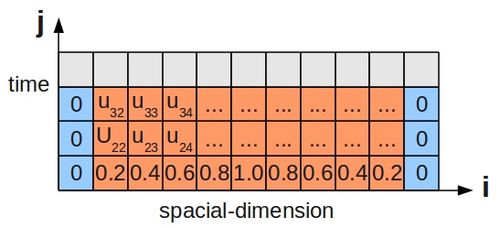
This describes purely diffusive phenomena and can give us the steady state temperature over a 2D plate, three sides of which are held at 100°C, while the fourth is held at 0°C. We have divided the plate into a number of grid cells:
Using the finite difference formulae that we derived in the last section, we can convert the differential equation into a difference equation:
- [math]\displaystyle{ \frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2} \approx \frac{1}{h^2}(u^j_{i+1} -2u^j_i +u^j_{i-1}) + \frac{1}{k^2}(u^{j+1}_i -2u^j_i +u^{j-1}_i) }[/math]
where h is the grid spacing in the i-directions and k is the spacing the j-direction. If we set [math]\displaystyle{ h=k }[/math], then:
- [math]\displaystyle{ u^j_{i+1} + u^j_{i-1} + u^{j+1}_i + u^{j-1}_i - 4u^j_i = 0 }[/math]
solving for [math]\displaystyle{ u^j_i }[/math]:
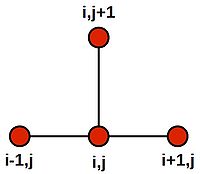
- [math]\displaystyle{ u^j_i = \frac{1}{4}(u^j_{i+1} + u^j_{i-1} + u^{j+1}_i + u^{j-1}_i) }[/math]
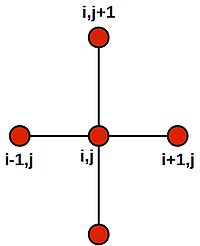
Note that this last equation says--quite intuitively--that the value at the central grid point is equal to the average of its four neighbours. We can draw a picture of the stencil needed to compute the value:
Placing the stencil on the 4 grid cells on the inner region (orange) in turn, we generate the following 4 difference equations:
- [math]\displaystyle{ \begin{alignat}{5} -4u_{22} & + u_{32} & + u_{23} & + 100 & + 100 & = 0 \\ -4u_{32} & + 0 & + u_{33} & + u_{22} & + 100 & = 0 \\ -4u_{23} & + u_{33} & + 100 & + 100 & + u_{22} & = 0 \\ -4u_{33} & + 0 & + 100 & + u_{23} & + u_{32} & = 0 \\ \end{alignat} }[/math]
This system of equations can be written in matrix form:
- [math]\displaystyle{ \begin{bmatrix}-4 & 1 & 1 & 0\\1 & -4 & 0 & 1\\1 & 0 & -4 & 1\\0 & 1 & 1 & -4\end{bmatrix} \begin{bmatrix}u_{22}\\u_{32}\\u_{23}\\u_{33}\end{bmatrix} = \begin{bmatrix}-200\\-100\\-200\\-100\end{bmatrix} }[/math]
Which may be summarised as the vector equation, Ax=b, which can be efficiently & conveniently solved using a library linear algebra routines, such as LAPACK, PETSc or PLASMA.
Parabolic Equations: Forward Euler
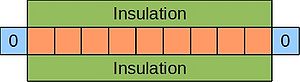
The 1D heat equation:
- [math]\displaystyle{ \frac{\partial u}{\partial t}=\alpha \frac{\partial^2u}{\partial x^2} }[/math]
where [math]\displaystyle{ \alpha }[/math]--the thermal diffusivity--is set to 1 for simplicity.
- [math]\displaystyle{ \frac{u^{j+1}_i - u^j_i }{k} = \frac{u^j_{i+1} - 2u^j_i + u^j_{i-1}}{h^2} }[/math]
- [math]\displaystyle{ u^{j+1}_i = u^j_i + r(u^j_{i+1} - 2u^j_i + u^j_{i-1}) }[/math]
where:
[math]\displaystyle{ r=\frac{k}{h^2} }[/math]
Parabolic Equations: Crank-Nicolson
The CFL condition:
- [math]\displaystyle{ r=\frac{k}{h^2} \le 0.5 }[/math]
for stability.
The 1D heat equation:
- [math]\displaystyle{ \frac{\partial u}{\partial t}=\alpha \frac{\partial^2u}{\partial x^2} }[/math]
where [math]\displaystyle{ \alpha }[/math]--the thermal diffusivity--is set to 1 for simplicity.
Create a finite difference equation using the Crank-Nicolson stencil:
- [math]\displaystyle{ \frac{u^{j+1}_i - u^j_i}{k} = \frac{1}{2}(\frac{u^{j+1}_{i+1} - 2u^{j+1}_{i} + u^{j+1}_{i-1}}{h^2} + \frac{u^j_{i+1} - 2u^j_i + u^j_{i-1}}{h^2}) }[/math]
rearrange,
- [math]\displaystyle{ u^{j+1}_i - u^j_i = \frac{1}{2}\frac{k}{h^2}(u^{j+1}_{i+1} - 2u^{j+1}_i + u^{j+1}_{i-1} + u^j_{i+1} - 2u^j_i + u^j_{i-1}) }[/math]
- [math]\displaystyle{ 2(u^{j+1}_i - u^j_i) = r(u^{j+1}_{i+1} - 2u^{j+1}_i + u^{j+1}_{i-1} + u^j_{i+1} - 2u^j_i + u^j_{i-1}) }[/math]
where [math]\displaystyle{ r=\frac{k}{h^2} }[/math]
collect the unknowns (values of u at the next timestep, i+1) to the LHS and the knowns (values of u at current timestep, i):
- [math]\displaystyle{ 2u^{j+1}_i + 2ru^{j+1}_i - ru^{j+1}_{i+1} - ru^{j+1}_{i-1} = 2u^j_i +ru^j_{i+1} -2ru^j_i + ru^j_{i-1} }[/math]
- [math]\displaystyle{ (2+2r)u^{j+1}_i - ru^{j+1}_{i+1} - ru^{j+1}_{i-1} = (2-2r)u^j_i +ru^j_{i+1} + ru^j_{i-1} }[/math]
if we choose [math]\displaystyle{ h=1/10 }[/math] and [math]\displaystyle{ k=1/100 }[/math], then [math]\displaystyle{ r=1 }[/math].