Difference between revisions of "R1"
| Line 125: | Line 125: | ||
</source> | </source> | ||
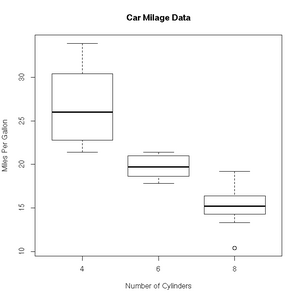
| − | [http://en.wikipedia.org/wiki/Box_plot 'Box and whisker' plots] are useful ways to graph the quartiles of some data. In this case, | + | [http://en.wikipedia.org/wiki/Box_plot 'Box and whisker' plots] are useful ways to graph the quartiles of some data. In this case, the fuel efficiencies of various US cars, circa 1974: |
<source> | <source> | ||
| Line 131: | Line 131: | ||
+ xlab="Number of Cylinders", ylab="Miles Per Gallon") | + xlab="Number of Cylinders", ylab="Miles Per Gallon") | ||
</source> | </source> | ||
| + | |||
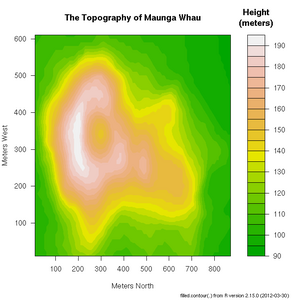
| + | R includes a very useful help facility. In the case of the '''filled.contour()''' plotting function, the help page includes an example of it's use to plot the topology of a volcano in Auckland, NZ: | ||
<source> | <source> | ||
Revision as of 14:16, 21 June 2013
Open Source Statistics with R
Introduction
R is a mature, open-source (i.e. free!) statistics package, with an intuitive interface, excellent graphics and a vibrant community constantly adding new methods for the statistical investigation of your data to the library of packages available.
The goal of this tutorial is to introduce you to the R package, and not to be an introductory course in statistics.
Some excellent examples of using R can also be found at: http://msenux.redwoods.edu/math/R/ and http://www.r-tutor.com/
Getting Started
The very simplest thing we can do with R is to perform some arithmetic at the command prompt:
> phi <- (1+sqrt(5))/2
> phi
[1] 1.618034Parentheses are used to modify the usual order of precedence of the operators (/ will typically be evaluated before +). Note the [1] accompanying the returned value. All numbers entered at the console are interpreted as a vector. The '[1]' indicates that the line in question is displaying the vector of values starting at first index. We can use the handy sequence function to create a vector containing more than a single element:
> odds <- seq(from=1, to=67, by=2)
> odds
[1] 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
[26] 51 53 55 57 59 61 63 65 67From the above example, we can see that both the <- and = operators can be used for assignment.
Vectors are commonly used data structures in R:
coords.bris <- c(51.5, 2.6)As are matrices:
> magic <- matrix(data=c(2,7,6,9,5,1,4,3,8),nrow=3,ncol=3)
> magic
[,1] [,2] [,3]
[1,] 2 9 4
[2,] 7 5 3
[3,] 6 1 8Where the c function combines the arguments given in the parentheses. We can access portions of the array using the syntax shown in the square brackets. For example, we can access the first row using the [1,] notation, and similarly the second column using [,2]. Since the square is 3x3 magic, the numbers in both slices should sum to 15:
> sum(magic[1,])
[1] 15
> sum(magic[,2])
[1] 15Single elements and ranges can also accessed:
> magic[2,2]
[1] 5
> magic[2:3,2:3]
[,1] [,2]
[1,] 5 3
[2,] 1 8R also provides arrays, which have more than two dimensions, and lists to hold heterogeneous collections.
A very commonly used data structure is the data frame, which R uses to store tabular data. Given several vectors of equal length, we can collate them into a data frame:
> countries <- c("USA", "China", "UK")
> golds <- c(46, 38, 29)
> silvers <- c(29, 27, 17)
> bronzes <- c(29, 23, 19)
> medals.2012 <- data.frame(countries, golds, silvers, bronzes)
> medals.2012
countries golds silvers bronzes
1 USA 46 29 29
2 China 38 27 23
3 UK 29 17 19Graphics: A taster
An aspect which makes R popular are it's graphing functions. R also has some very handy built-in data sets--we'll use this to demonstrate just a small fraction of R's graphing abilities.
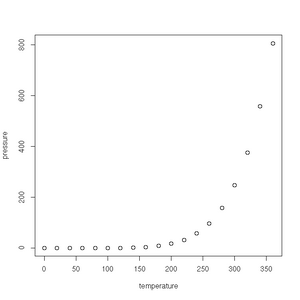
First up is the humble plot() function. Given a data frame of points, such as one charting the relationship between temperature and the vapour pressure of mercury, it will give us a (handily labelled) scatter plot:
> plot(pressure)See the gallery below for all the plots created in this section.
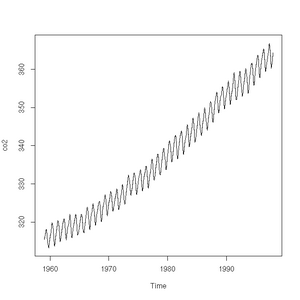
The plot function will also accept a time-series (another class of object recognised by R) and will sensibly join the points with a line:
> plot(co2)
> class(co2)
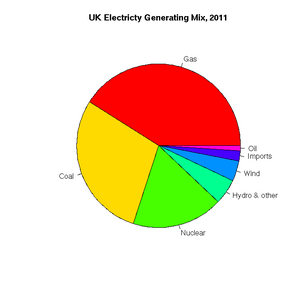
[1] "ts"Pie charts are easily constructed. In this case, to show the relative proportions of electricity generated from different sources in the UK in 2011 (source: https://www.gov.uk/government/.../5942-uk-energy-in-brief-2012.pdf):
> uk.electricty.sources.2011 <- c(41,29,18,5,4,2,1)
> names(uk.electricty.sources.2011) <- ("Gas", "Coal", "Nuclear", "Hydro & other", "Wind", "Imports", "Oil")
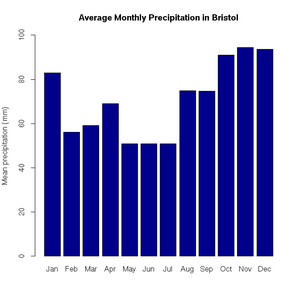
> pie(uk.electricty.sources.2011, main="UK Electricty Generating Mix, 2011", col=rainbow(7))Next, let's create a bar chart of monthly average precipitation falling here in the fair city of Bristol (source: http://www.worldweatheronline.com):
> bristol.precip <- c(82.9, 56.1, 59.2, 69, 50.8, 50.9, 50.8, 74.8, 74.7, 91.1, 94.5, 93.6)
> names(bristol.precip) <- c("Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec")
> barplot(bristol.precip,
+ main="Average Monthly Precipitation in Bristol",
+ ylab="Mean precipitation (mm)",
+ ylim=c(0,100),
+ col=c("darkblue"))'Box and whisker' plots are useful ways to graph the quartiles of some data. In this case, the fuel efficiencies of various US cars, circa 1974:
> boxplot(mpg~cyl,data=mtcars, main="Car Milage Data",
+ xlab="Number of Cylinders", ylab="Miles Per Gallon")R includes a very useful help facility. In the case of the filled.contour() plotting function, the help page includes an example of it's use to plot the topology of a volcano in Auckland, NZ:
> ?filled.countourData Structures
Packages
Examples of Common Tasks
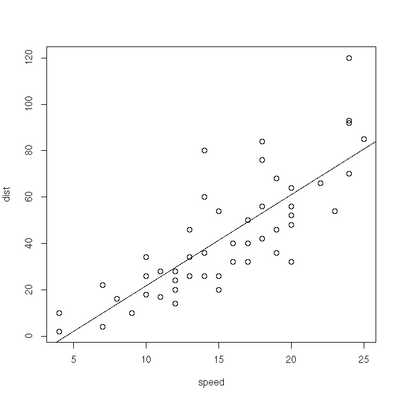
Linear Regression
> plot(cars)
> res=lm(dist ~ speed, data=cars)
> abline(res)Exercise
- Weighted least squares. The lm function will accept a vector of weights, lm(... weights=...). If given, the function will optimise the line of best fit according a the equation of weighted least squares. Experiment with different linear model fits, given different weighting vectors. Some handy hints for creating a vector of weights:
- w1<-rep(0.1,50) will give you a vector, length 50, where each element has a value of 0.1. W1[1]<-10 will give the first element of the vector a value of 10.
- w2<-seq(from=0.02, to=1.0, by=0.02) provides a vector containing a sequence of values from 0.02 to 1.0 in steps of 0.02 (handily, again 50 in total).
Significance Testing
> boys_2=c(90.2, 91.4, 86.4, 87.6, 86.7, 88.1, 82.2, 83.8, 91, 87.4)
> girls_2=c(83.8, 86.2, 85.1, 88.6, 83, 88.9, 89.7, 81.3, 88.7, 88.4)
> res=var.test(boys_2,girls_2)
> res=t.test(boys_2, girls_2, var.equal=TRUE, paired=FALSE)