Difference between revisions of "LinAlgebraPacks"
| Line 2: | Line 2: | ||
'''Packages for Linear Algebra: Solving your system of equations using (optimised, bug-free) code that someone else has already written!''' | '''Packages for Linear Algebra: Solving your system of equations using (optimised, bug-free) code that someone else has already written!''' | ||
| + | =Introduction= | ||
| − | + | A number of example programs highlighting the use of linear algebra packages, such as LAPACK, PETSc, PLASMA and MAGMA, will be described on this page. The examples are typically based upon the solution of a partial differential equation (PDE) using the Finite Difference Method (FDM). The theory of the FDM is described on [[NumMethodsPDEs]]. | |
| + | |||
| + | To download the source code for the examples, you can type: | ||
<source> | <source> | ||
Revision as of 11:22, 13 April 2011
Packages for Linear Algebra: Solving your system of equations using (optimised, bug-free) code that someone else has already written!
Introduction
A number of example programs highlighting the use of linear algebra packages, such as LAPACK, PETSc, PLASMA and MAGMA, will be described on this page. The examples are typically based upon the solution of a partial differential equation (PDE) using the Finite Difference Method (FDM). The theory of the FDM is described on NumMethodsPDEs.
To download the source code for the examples, you can type:
svn co https://svn.ggy.bris.ac.uk/subversion-open/num-methods1 ./num-methods1LAPACK:direct solutions for dense matrices
For example, consider the following system of linear equations:
- [math]\displaystyle{ \begin{alignat}{7} x &&\; + \;&& 3y &&\; - \;&& 2z &&\; = \;&& 5 & \\ 3x &&\; + \;&& 5y &&\; + \;&& 6z &&\; = \;&& 7 & \\ 2x &&\; + \;&& 4y &&\; + \;&& 3z &&\; = \;&& 8 & \end{alignat} }[/math]
(From http://en.wikipedia.org/wiki/System_of_linear_equations.)
The following computation shows Gauss-Jordan elimination applied to the matrix version (Ax=b) of the above system:
- [math]\displaystyle{ \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 0 & -4 & 12 & -8 \\ 2 & 4 & 3 & 8 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 0 & -4 & 12 & -8 \\ 0 & -2 & 7 & -2 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 0 & 1 & -3 & 2 \\ 0 & -2 & 7 & -2 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 0 & 1 & -3 & 2 \\ 0 & 0 & 1 & 2 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & 0 & 9 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \end{array}\right]. }[/math]
cd num-methods1/examples/example1
To solve this using LAPACK take a look inside dgesv-example.f90. First the declarations:
integer, parameter :: N = 3
integer, parameter :: LDA = N ! leading dimension of A
integer, parameter :: LDB = N ! leading dimension of B
integer, parameter :: NRHS = 1 ! no. of RHS, i.e columns in b
integer, dimension(N) :: IPIV
integer :: INFO
integer :: i
real(kind=8), dimension(LDA,N) :: A ! LDAxN matrix
real(kind=8), dimension(LDB,NRHS) :: B ! LDBxNRHS matrix
Next, we set up the matrix A:
! ( 1 3 -2)
! ( 3 5 6)
! ( 2 4 3)
A(1,1) = 1.0d+0
A(1,2) = 3.0d+0
A(1,3) = -2.0d+0
A(2,1) = 3.0d+0
A(2,2) = 5.0d+0
A(2,3) = 6.0d+0
A(3,1) = 2.0d+0
A(3,2) = 4.0d+0
A(3,3) = 3.0d+0
And the vector B:
! ( 5)
! ( 7)
! ( 8)
B(1,1) = 5.0d+0
B(2,1) = 7.0d+0
B(3,1) = 8.0d+0
Once we have all that in place, all we need to do is call the solver routine. (Note that the solution vector replaces the values in B):
call dgesv(N, NRHS, A, LDA, IPIV, B, LDB, INFO)
Run the program to satisfy yourself that it works:
cd num-methods1/examples/example1 make ./dgesv-example.exe
Next, take a look at simple-laplace.f90. This program solves the 2D laplace equation for a 4x4 domain, as described on NumMethodsPDEs. This program only differs from the previous one in way in which we initialise the matrix A and vector b. To run the program type:
./simple-laplace-expert.exe
mxm-laplace.f90 also solves our laplacian example, except that this time we can vary the size of the matrix and corresponding arrays for an mxm square domain:
./mxm-laplace.exe
LAPACK also gives us access to a routine--dgesvx--which solves the same system of equations, but also gives us some error analysis. The x stands for expert.
./mxm-laplace.exe
Direct Solve using LU Decomposition
In practice, the LAPACK routine dgesv does not perform Gaussian elimination, but rather computes an LU decomposition and then solves the equation using two substitution steps--one forward and one backward. This is because for the same computational cost, we can factor A without knowing about b. We can then find x cheaply, for many different b. This is useful when solving parabolic equations, where x at time-step [math]\displaystyle{ j }[/math] forms the basis for b at time-step [math]\displaystyle{ j+1 }[/math].
OK, how to we obtain an LU decomposition?
The Guassian elimination process above can be expressed as a matrix multiplication. The elimination in the first column can be achieved by left multiplying A with a unit (1's on the diagonal) lower triangular matrix, [math]\displaystyle{ L_1 }[/math], with non-zeros only in the first column (this case is called an atomic unit lower triangular matrix), such as that schematically shown below:
- [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 \\ x & 1 & 0 \\ y & 0 & 1 \end{bmatrix} }[/math]
Following our example, [math]\displaystyle{ L_1 A=A' }[/math] becomes:
- [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 3 & -2 \\ 3 & 5 & 6 \\ 2 & 4 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & -2 & 7 \end{bmatrix} }[/math]
The eliminations in the second column are achieved by left multiplying [math]\displaystyle{ A'=L_1 A }[/math] by [math]\displaystyle{ L_2 }[/math] (which is atomic unit lower triangular with non-zeros only in the second column):
- [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -\frac{1}{2} & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 3 & -2 \\ 3 & 5 & 6 \\ 2 & 4 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & 0 & 1 \end{bmatrix} }[/math]
We note that the result [math]\displaystyle{ L_2 L_1 A = A'' = U }[/math] is upper triangular. Rearranging we get, [math]\displaystyle{ A=L_1^{-1} \cdots L^{-1}_{n-2} L^{-1}_{n-1} U }[/math]. The inverse matrices, [math]\displaystyle{ L^{-1} }[/math], are very easy to find as the inverse of an atomic unit lower triangular matrix is the same as the original save only for a change of sign in the off diagonal elements. The product is, again, unit lower triangular. Thus [math]\displaystyle{ A=LU }[/math]:
- [math]\displaystyle{ \begin{bmatrix} 1 & 3 & -2 \\ 3 & 5 & 6 \\ 2 & 4 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & \frac{1}{2} & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 2 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 2 & \frac{1}{2} & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & 0 & 1 \end{bmatrix} }[/math]
Given L and U we can solve [math]\displaystyle{ Ax=b }[/math] by first solving:
- [math]\displaystyle{ Ly=b }[/math].
As L is unit lower triangular, we can do this by easily by forward substitution. Once we know y, we can solve:
- [math]\displaystyle{ Ux=y }[/math],
easily again, this time by backward substitution.
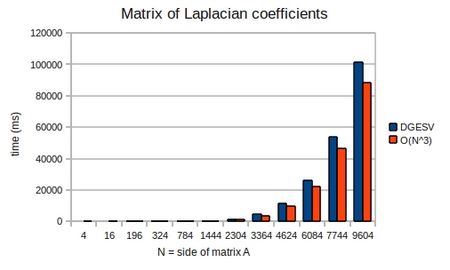
Computing the LU decomposition of an [math]\displaystyle{ n \times n }[/math] system of equations has a computational cost of [math]\displaystyle{ O(n^3) }[/math] operations, whereas the forward and backward substitution steps have a cost of [math]\displaystyle{ O(n^2) }[/math] operations. Thus the cost of solution is dominated by the LU decomposition.
To demonstrate that the solution does indeed take [math]\displaystyle{ O(n^3) }[/math] operations, I ran mxm-laplacian.exe on my desktop PC for varying sizes of N and could plot the following from the results:
If we look once again at dgesv-example.f90 and set:
logical, parameter :: verbose=.true.
(and recompile and run) we can see the contents of A after the call to dgesv(). It now contains an encoding of the LU decomposition (the unit leading diagonal from L is assumed):
LU decomposition as encoded in matrix A:
3.00000000000000 5.00000000000000 6.00000000000000
0.333333333333333 1.33333333333333 -4.00000000000000
0.666666666666667 0.500000000000000 1.00000000000000
..and the IPIV vector:
2 2 3
This is all well and good, but hang-on a cotton pickin' minute, the matrix U is not as we expected:
- [math]\displaystyle{ \begin{bmatrix} 3 & 5 & 6 \\ 0 & \frac{4}{3} & -4 \\ 0 & 0 & 1 \end{bmatrix} \neq \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & 0 & 1 \end{bmatrix} }[/math]
Why not? The answer lies the in contents of the IPIV. The elements along the leading diagonal are known as pivots. If any pivots are small, our algorithm will become unstable. We may exchange rows (known as partial pivoting) in A without changing the solution. The way to read IPIV is that value j of the ith entry indicates that row i was exchanged with row j. In the case above, row one was exchanged with row 2, but then rows 2 and 3 were kept the same. This upshot of this maneuver is that we moved a 1 from the leading diagonal and replaced it with a 3.
We can satisfy ourselves that all is well, by factorising this permuted matrix:
- [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & \frac{1}{2} & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 \\ \frac{1}{3} & 1 & 0 \\ \frac{2}{3} & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 3 & 5 & 6 \\ 0 & \frac{4}{3} & -4 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 3 & 5 & 6 \\ 1 & 3 & -2 \\ 2 & 4 & 3 \end{bmatrix} }[/math]
Our second example uses a pre-computed LU decomposition when solving a parabolic equation using the Crank-Nicolson scheme.
cd ../example2
In simple-crank-nicolson.f90 we see that the initial call to dgesv replaces the entries in the matrix A with an encoding of the LU decompostion (the unit diagonal is assumed). For subsequent timesteps we can thus call dgetrs instead:
do ii=2,4
...
call dgetrs('N', N, NRHS, A, LDA, IPIV, B, LDB, INFO)
...
end do
where we have remembered to take account of the boundary conditions at each time-step too:
do ii=2,4
...
! copy B into B1, so that we can recompute for
! the boundary conditions again.
B1 = B
! Need to recalculate entries for the vector of known
! values--held in B--given the solution at the current
! timestep--held in B1.
! *NB* the loops below are only valid for the case r=1.
! LHS
B(1,1) = 0 + B1(2,1)
! RHS
B(N,1) = 0 + B1(N-1,1)
! middle bit
do jj=2,N-1
B(jj,1) = B1(jj-1,1) + B1(jj+1,1)
end do
...
end do
Exercises
- example2 also contains simple programs to compute the forward- and backward-Euler schemes using LAPACK subroutine calls (see NumMethodsPDEs). Experiment with values of [math]\displaystyle{ r=\frac{k}{h^2} }[/math] for the 3 schemes, so as to highlight the effects of the CFL condition.
Banded Matrices
In all my examples, thus far, I've called routines from the dgexxx series offered by LAPACK. The d stands for double and the ge for generel purpose. For banded matrices, LAPACK offers a much more efficient format and routines to match. Take a look at http://www.netlib.org/lapack/double/ for a list of driver routines using matrices of double precision numbers, or http://www.netlib.org/lapack for more documentation in general.
PetSc: Iterative solutions and sparse matrices
In order to compute the solution of a linear system via the direct method of an LU-decomposition, we know that it will cost [math]\displaystyle{ O(n^3) }[/math] operations. Can we compute a solution more cheaply? The class of iterative methods strive to compute a cheaper solution by first guessing a value for the solution vector [math]\displaystyle{ x }[/math] and then iteratively refining it. Thus we will get a series of (hopefully!) improving approximations:
- [math]\displaystyle{ x^0, x^1, x^2, x^3, \cdots, x^j \rightarrow x }[/math]
By way of an illustration of such a method, consider splitting matrix A into 3 others:
- [math]\displaystyle{ A = L + D + U }[/math]
Note the summation, and so the L and the U matrices are not the same as those considered in the LU-decomposition used by the direct approach. With this split, [math]\displaystyle{ Ax=b }[/math], becomes:
- [math]\displaystyle{ Lx + Dx + Ux = b }[/math]
The game now is to replace some occurrences of [math]\displaystyle{ x }[/math] by [math]\displaystyle{ x^k }[/math] and others by [math]\displaystyle{ x^{k+1} }[/math], and thereby obtaining a relationship which tells us how to get an approximation at one iteration step, from the approximation at the previous step. If the resulting iterative scheme converges, then we're in business!
One classic form of such an iteration is the Jacobi method (which is useful when A is diagonally dominant):
- [math]\displaystyle{ Lx^j + Dx^{j+1} + Ux^j = b }[/math]
- [math]\displaystyle{ x^{j+1} = D^{-1}(b - (L + U)x^j) }[/math]
To take a look at a illustrative implementation of the Jacobi method using LAPACK:
cd ../example3 make
and take a look at jacobi-example.f90. To run the executable, type:
./jacobi-example.exe
Happily, however, we do not need to write our own iterative schemes, as the good folk at Argonne have written the PETSc library.
http://www.mcs.anl.gov/petsc/petsc-as/
Take a look inside ex1f.F to see how to solve our laplacian example using PETSc. To run the program type:
./ex1f
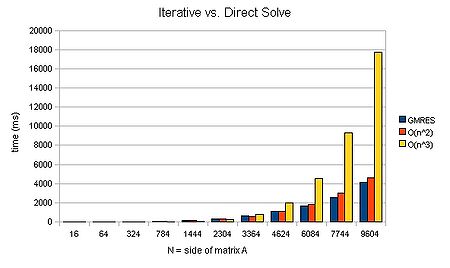
We can again plot a graph of timings given varying N:
We can see that an iterative method can scale approximately [math]\displaystyle{ O(n^2) }[/math]. For large matrices, this can mean that a solution is found several orders of magnitude faster. Now that is a speed-up worth having! It's liking buying a supercomputer than runs several orders of magnitude faster than your old one..
Better yet, you can try different schemes for iterative solution, just by varying some command-line arguments. For example:
./ex1f -ksp_type bcgs -pc_type jacobi
will invoke the biconjugate gradient stabalised scheme together with a jacobi preconditioner matrix. (This in fact runs faster than the GMRES method for the above case--808ms for N=9694. Note, however, that it cannot scale better than [math]\displaystyle{ O(N^2) }[/math].) For those interested, the PETSc manual is the best next port of call for more details on the various methods made available by the package.
For further examples see INSTALL_DIR/petsc-3.1-p1/src/ksp/ksp/examples/tutorials.
PLASMA: For Multicore Architectures
http://icl.cs.utk.edu/plasma/index.html
cd ../example4 make ./mxm-laplace-plasma.exe
For further examples, see e.g. INSTALL_DIR/plasma-installer_2.3.1/build/plasma_2.3.1.