Difference between revisions of "Profiling"
| Line 245: | Line 245: | ||
* Avoid loops, especially in interpreted languages (like R). | * Avoid loops, especially in interpreted languages (like R). | ||
| − | |||
| − | |||
==A Common Situation Involoving Loops== | ==A Common Situation Involoving Loops== | ||
Revision as of 12:31, 22 July 2013
Can I speed up my program?
Introduction
Are you in the situation where you wrote a program or script which worked well on a test case but now that you scale up your ambition, your jobs are taking an age to run? If so, then the information below is for you!
Key Questions
Now that we have established that you'd like your jobs to run more quickly, here are the some key questions that you will want to address:
- How long, exactly, does my program take to run?
- Is there anything I can do to speed it up?
- Which parts of my program take up most of the execution time?
- Where should I focus my improvement efforts?
We'll get onto answering these questions in a moment. First, however, it is essential that we go into battle fully informed. The next section outlines some key concepts when thinking about program performance. These will help focus our minds when we go looking for opportunities for a speed-up.
Factors which Impact on Performance
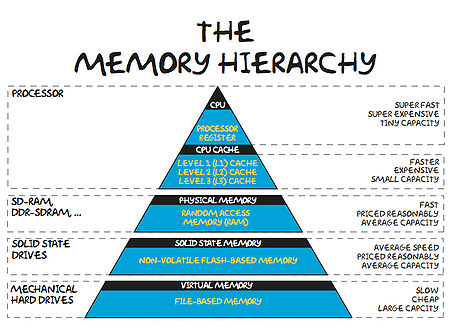
The Memory Hierarchy
These days, it takes much more time to move some data from main memory to the processor, than it does to perform operations on that data. In order to combat this imbalance, computer designers have created intermediate caches for data between the processor and main memory. Data stored at these staging posts may be accessed much more quickly than that in main memory. However, there is a trade-off, and caches have much less storage capacity than main memory.
An analogy helps us appreciate the relative differences between various storage locations:
| L1 Cache | Picking up a book off your desk (~3s) |
| L2 Cache | Getting up and getting a book off a shelf (~15s) |
| Main Memory | Walking down the corridor to another room (several minutes) |
| Disk | Walking the coastline of Britain (about a year) |
Now, it is clear that a program which is able to find the data it needs in cache will run much faster than one which regularly reads data from main memory (or worse still, disk).
How can we ensure that we make best use of the memory hierarchy?
Starting at the slowest end: Let's suppose you have a data set stored on disk which you want to work on. If that data will all fit into main memory, then it will very likely pay dividends to read all this data at the outset, work on it, and then save out any results to disk at the end. This is especially true if you will access all of the data items more than once or will have a non-contiguous pattern of access.
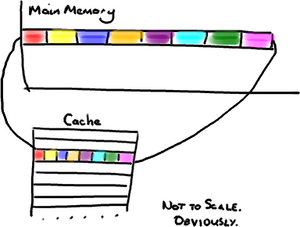
Ensuring that we make best use of cache is a little more subtle. In order to devise a good strategy, we must appreciate some of the hidden details of the inner workings of a computer: Let's say a program requests to read a single item from memory. First, the computer will look for the item in cache. If the data is not found in cache, it will be fetched from main memory, so as to create a more readily accessible copy. Single items are not fetched, however. Instead chunks of data are copied into cache. The size of this chunk matches the size of a block of storage in cache known as a cache line (often 64 bytes in today's machines). The situation is a little more complex when writing, as we have to ensure that both cache and main memory are synchronised, but--in the interests of brevity--we'll skip over this just now.
The pay-off for this chunked approach is that if the program now requests to read another item from memory, and that item was part of the previous fetch, then it will already be in cache and an slow journey to main memory will be avoided. Thus we can see that re-use of data already in cache will be a key factor in program performance.
A good example of this would be a looping situation. A loop order which predominately cycles over items already in cache will run much faster than one which demands that cache is constantly refreshed. Another point to note is that cache size is limited, so a loop cannot access many large arrays with impunity. Using too many arrays in a single loop will exhaust cache capacity and force evictions and subsequent re-reads of essential items.
Optimising Compilers
Compilers take the (often English-like) source code that we write and convert it into a binary code that can be comprehended by a computer. However, this is no trivial translation. Modern optimising compilers can essentially re-write large chunks of your code, keeping it semantically the same, but in a form which will execute much, much faster (we'll see examples below). To give some examples, they will spit of join loops, they will hoist repeated, invariant calculations out of loops, re-phrase your arithmetic etc. etc.
In short, they are very, very clever. And it does not pay to second guess what your compiler will do. It is sensible to:
- Use all the appropriate compiler flags you can think of (see e.g. https://www.acrc.bris.ac.uk/pdf/compiler-flags.pdf) to make your code run faster, but also to:
- Use a profiler to determine which parts of your executable code (i.e. post compiler transformation) are taking the most time.
That way, you can target any improvement efforts on areas that will make a difference!
Exploitation of Modern Processor Architectures
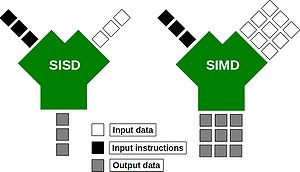
Just like the compilers described above. Modern processors are complex beasts! Over recent years, they have been evolving so as to provide more number crunching capacity, without using more electricity. One way in which they can do this is through the use of wide registers and the so-called SIMD (Single Instruction, Multiple Data) execution model:
Wide-registers allow several data items of the same type to be stored, and more importantly, processed together. In this way, a modern SIMD processor may be able to operate on 4 double-precision floating point numbers concurrently. What this means for you as a programmer, is that if you phrase your loops appropriately, you may be able to perform several of your loop interactions at the same time. Possibly saving you a big chunk of time.
Suitably instructed (often -O3 is sufficient), those clever-clog compilers will be able to spot areas of code that can be run using those wide registers. The process is called vectorisation. Today's compilers can, for example, vectorise loops with independent iterations (i.e. no data dependencies from one iteration to the next). You should also avoid aliased pointers (or those that cannot be unambiguously identified as un-aliased).
Modern processors have also evolved to have several (soon to be many!) CPU cores on the same chip:
Many cores means that we can invoke many threads or processes, all working within the same, shared memory space. Don't forget, however, that if these cores are not making the best use of the memory hierarchy, or there own internal wide-registers, you will not be operating anywhere near the full machine capacity. So you are well advised to consider the above topics before racing off to write parallel code.
Tools for Measuring Performance
gprof
gcc -O3 -ffast-math -pg d2q9-bgk.c -o d2q9-bgk.exe
gprof d2q9-bgk.exe gmon.out
Flat profile: Each sample counts as 0.01 seconds. % cumulative self self total time seconds seconds calls ms/call ms/call name 49.08 31.69 31.69 10000 3.17 3.17 collision 33.87 53.56 21.87 10000 2.19 2.19 propagate 17.13 64.62 11.06 main 0.00 64.62 0.00 1 0.00 0.00 initialise 0.00 64.62 0.00 1 0.00 0.00 write_values
TAU
On BCp1:
> module av tools/tau tools/tau-2.21.1-intel-mpi tools/tau-2.21.1-openmp tools/tau-2.21.1-mpi
On BCp2:
> module add profile/tau profile/tau-2.19.2-intel-openmp profile/tau-2.19.2-pgi-mpi profile/tau-2.19.2-pgi-openmp profile/tau-2.21.1-intel-mpi
> module add profile/tau-2.19.2-intel-openmp
Want to compile some C code:
tau_cc.sh -O3 d2q9-bgk.c -o d2q9-bgk.exe
> pprof profile.0.0.0
Reading Profile files in profile.*
NODE 0;CONTEXT 0;THREAD 0:
---------------------------------------------------------------------------------------
%Time Exclusive Inclusive #Call #Subrs Inclusive Name
msec total msec usec/call
---------------------------------------------------------------------------------------
100.0 21 2:00.461 1 20004 120461128 int main(int, char **) C
91.5 58 1:50.231 10000 40000 11023 int timestep(const t_param, t_speed *, t_speed *, int *) C
70.8 1:25.276 1:25.276 10000 0 8528 int collision(const t_param, t_speed *, t_speed *, int *) C
19.8 23,846 23,846 10000 0 2385 int propagate(const t_param, t_speed *, t_speed *) C
8.3 10,045 10,045 10001 0 1004 double av_velocity(const t_param, t_speed *, int *) C
0.8 1,016 1,016 10000 0 102 int rebound(const t_param, t_speed *, t_speed *, int *) C
0.1 143 143 1 0 143754 int write_values(const t_param, t_speed *, int *, double *) C
0.0 34 34 10000 0 3 int accelerate_flow(const t_param, t_speed *, int *) C
0.0 18 18 1 0 18238 int initialise(t_param *, t_speed **, t_speed **, int **, double **) C
0.0 0.652 0.652 1 0 652 int finalise(const t_param *, t_speed **, t_speed **, int **, double **) C
0.0 0.002 0.572 1 1 572 double calc_reynolds(const t_param, t_speed *, int *) C
Valgrind
Valgrind is an excellent open-source tool for debugging and profiling.
Compile your program as normal, adding in any optimisation flags that you desire, but also add the -g flag so that valgrind can report useful information such as line numbers etc. Then run it through the callgrind tool, embedded in valgrind:
valgrind --tool=callgrind your-program [program options]
When your program has run you find a file called callgrind.out.xxxx in the current directory, where xxxx is replaced with a number (the process ID of the command you have just executed).
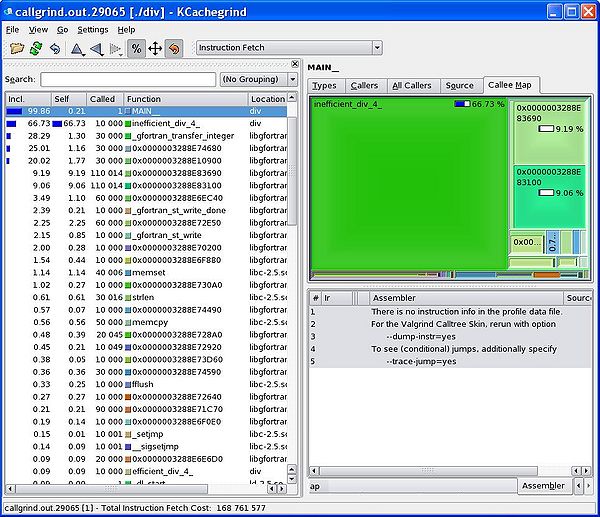
You can inspect the contents of this newly created file using a graphical display too call kcachegrind:
kcachegrind callgrind.out.xxxx
(For those using Enterprise Linux, you call install valgrind and kcachegrind using yum install kdesdk valgrind.)
A Simple Example
svn co https://svn.ggy.bris.ac.uk/subversion-open/profiling/trunk ./profiling cd profiling/examples/example1 make valgrind --tool=callgrind ./div.exe >& div.out kcachegrind callgrind.out.xxxx
We can see from the graphical display given by kcachegrind that our inefficient division routine takes far more of the runtime that our efficient routine. Using this kind of information, we can focus our re-engineering efforts on the slower parts of our program.
The Matlab Profiler
- See http://www.mathworks.co.uk/help/matlab/ref/profile.html
- See also tic, toc timing: http://www.mathworks.co.uk/help/matlab/ref/tic.html
The Python Profiler
- http://www.huyng.com/posts/python-performance-analysis/
- http://www.appneta.com/2012/05/21/profiling-python-performance-lineprof-statprof-cprofile/
OK, but how do I make my code run faster?
OK, let's assume that we've located a region of our program that is taking a long time. So far so good, but how can we address that? There are--of course--a great many reasons why some code may take a long time to run. One reason could be just that it has a lot to do! Let's assume, however, that the code can be made to run faster by applying a little more of the old grey matter. With this in mind, let's consider a few common examples of code which can tweaked to run faster.
Compiler Options
You probably want to make sure that you've added all the go-faster flags that are available before you embark on any profiling. Activating optimisations for speed can make your progam run a lot faster!
As mentioned earlier, see e.g. https://www.acrc.bris.ac.uk/pdf/compiler-flags.pdf, for tips on which options to choose.
gcc d2q9-bgk.c -o d2q9-bgk.exe
time ./d2q9-bgk.exe
real 4m34.214s user 4m34.111s sys 0m0.007s
gcc -O3 d2q9-bgk.c -o d2q9-bgk.exe
real 2m1.333s user 2m1.243s sys 0m0.011s
gcc -O3 -ffast-math d2q9-bgk.c -o d2q9-bgk.exe
real 1m9.068s user 1m8.856s sys 0m0.012s
Scripting Languages
- Avoid loops, especially in interpreted languages (like R).
A Common Situation Involoving Loops
For our first example, consider the way we loop over the contents of a 2-dimensional array--a pretty common situation!. Skip over a directory and compile the example programs:
cd ../example2 make
In this directory, we have two almost identical programs. Compare the contents of loopingA.f90 and loopingB.f90. You will see that inside each program a 2-dimensional array is declared and two nested loops are used to visit each of the cells of the array in turn (and an arithmetic value is dropped in). The only way in which the two programs differ is the order in which the cycle through the contents of the arrays. In loopingA.f90, the outer loop is over the columns of the array and the inner loop is over the rows (i.e. for a given value of ii, all values of jj and cycled over). The opposite is true for loopingB.f90.
Let's compare how long it takes these two programs to run. We can do this using the Linux time command:
time ./loopingA.exe
and now,
time ./loopingB.exe
Dude! loopingA.exe takes more than twice the time of loopingB.exe. What's the reason?
Well, Fortran stores it's 2-dimensional arrays in column-major order. Our 2-dimension array is actually stored in the computer memory as a 1-dimension array, where the cells in a given column are next to each other. For example, the array:
- [math]\displaystyle{ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} }[/math]
would actually be stored in memory as:
1 4 2 5 3 6
That means is that our outer loop should be over the columns, and our inner loop over the rows. Otherwise we would end up hopping all around the memory, which takes extra time, and explains why loopingA takes longer.
The opposite situation is true for the C programming language, which stores its 2-dimensional arrays in row-major order. You can type:
make testC
To run some equivalent C code examples.
Not Doing the Same Thing Twice (or more!)
The following is the Manning formula drawn from the field of hydrology:
- [math]\displaystyle{ V = \frac{1}{n} R_h ^\frac{2}{3} \cdot S^\frac{1}{2} }[/math]
where:
[math]\displaystyle{ V }[/math] is the cross-sectional average velocity (m/s) [math]\displaystyle{ n }[/math] is the Gauckler–Manning coefficient (independent of units) [math]\displaystyle{ R_h }[/math] is the hydraulic radius (m) [math]\displaystyle{ S }[/math] is the slope of the water surface or the linear hydraulic head loss (m/m) ([math]\displaystyle{ S=h_f/L }[/math])
A program to compute estimates of [math]\displaystyle{ V }[/math], given an array of N hydraulic radii may contain the following loop:
do ii=1,N
V(ii) = (1/n) * (R(n)**(2.0/3.0)) * sqrt(S)
end do
However, this loop may be rather wasteful. For example, if the value for the Gauckler–Manning coefficient, [math]\displaystyle{ n }[/math] is the same for all the hydraulic radii, we would be computing (1/n) needlessly each time through the loop and could take it outside:
n_inv = (1/n)
do ii=1,N
V(ii) = n_inv * (R(n)**(2.0/3.0)) * sqrt(S)
end do
This would make particular sense, since the division operator is an expensive one. We also don't need to compute (2.0/3.0)) over and over:
n_inv = (1/n)
exponent=2.0/3.0
do ii=1,N
V(ii) = n_inv * (R(n)**exponent) * sqrt(S)
end do
Lastly, if the slope of the water surface is constant, then the square-root in the loop is also superfluous:
n_inv = (1/n)
exponent=2.0/3.0
root_S = sqrt(S)
do ii=1,N
V(ii) = n_inv * (R(n)**exponent) * root_S
end do
Now, modern optimising compilers are getting better and better at spotting this sort of thing and may actually create machine code from the first example which is as if you had made all the subsequent improvements. This is partly why we profile our programs in the first place, as it is very difficult to second guess what the compiler will do with your source code.
With that as a caveat it is worth just briefly listing typically expensive operations (in terms of CPU cycles) which a profile may point you too and which you may be able to address through some programming tweaks:
- memory operations such as allocate in Fortran, or malloc in C
- sqrt, exp and log
- division and raising raising numbers to a power
It's difficult to make sweeping statements in the area of code optimisation, but it will certainly pay not to do the same thing twice (or more!), especially is that thing is a relatively expensive operation.