Difference between revisions of "R1"
| Line 31: | Line 31: | ||
From the above example, we can see that both the '''<-''' and '''=''' operators can be used for assignment. | From the above example, we can see that both the '''<-''' and '''=''' operators can be used for assignment. | ||
| − | |||
| − | |||
| − | |||
=Graphics: A taster= | =Graphics: A taster= | ||
| Line 85: | Line 82: | ||
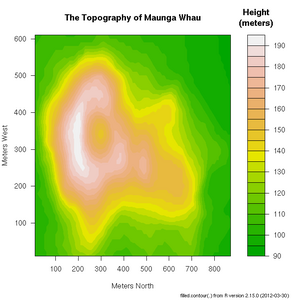
File:Maunga-Whau.png|Topology of Maunga Whau volcano in Auckland | File:Maunga-Whau.png|Topology of Maunga Whau volcano in Auckland | ||
</gallery> | </gallery> | ||
| + | |||
| + | =Data Structures= | ||
| + | |||
| + | =Packages= | ||
| + | |||
=Examples of Common Tasks= | =Examples of Common Tasks= | ||
| Line 113: | Line 115: | ||
> res=t.test(boys_2, girls_2, var.equal=TRUE, paired=FALSE) | > res=t.test(boys_2, girls_2, var.equal=TRUE, paired=FALSE) | ||
</source> | </source> | ||
| + | |||
| + | =Further Reading= | ||
| + | |||
| + | * [http://shop.oreilly.com/product/9780596801717.do| R in a Nutshell] | ||
Revision as of 13:29, 21 June 2013
Open Source Statistics with R
Introduction
R is a mature, open-source (i.e. free!) statistics package, with an intuitive interface, excellent graphics and a vibrant community constantly adding new methods for the statistical investigation of your data to the library of packages available.
The goal of this tutorial is to introduce you to the R package, and not to be an introductory course in statistics.
Some excellent examples of using R can also be found at: http://msenux.redwoods.edu/math/R
Getting Started
The very simplest thing we can do with R is to perform some arithmetic at the command prompt:
> phi <- (1+sqrt(5))/2
> phi
[1] 1.618034Parentheses are used to modify the usual order of precedence of the operators (/ will typically be evaluated before +). Note the [1] accompanying the returned value. All numbers entered at the console are interpreted as a vector. The '[1]' indicates that the line in question is displaying the vector of values starting at first index. We can use the handy sequence function to create a vector containing more than a single element:
> odds <- seq(from=1, to=67, by=2)
> odds
[1] 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
[26] 51 53 55 57 59 61 63 65 67From the above example, we can see that both the <- and = operators can be used for assignment.
Graphics: A taster
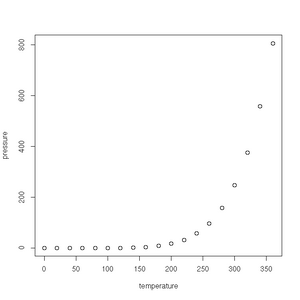
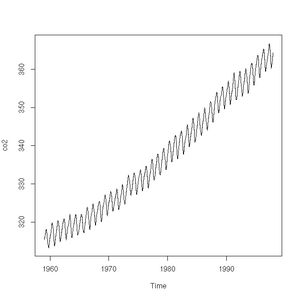
R has some very handy built-in data sets. They allow us to, for example, very simply plot the carbon dioxide concentrations as observed from 1959 to 1997 high above Hawaii at the Mauna Loa observatory.
> plot(pressure)> plot(co2)
> class(co2)
[1] "ts"https://www.gov.uk/government/.../5942-uk-energy-in-brief-2012.pdf
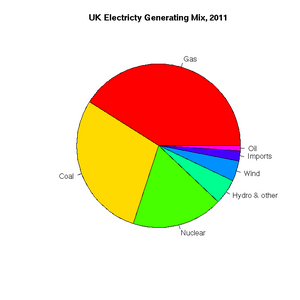
> uk.electricty.sources.2011 <- c(41,29,18,5,4,2,1)
> names(uk.electricty.sources.2011) <- ("Gas", "Coal", "Nuclear", "Hydro & other", "Wind", "Imports", "Oil")
> pie(uk.electricty.sources.2011, main="UK Electricty Generating Mix, 2011", col=rainbow(7))http://www.worldweatheronline.com
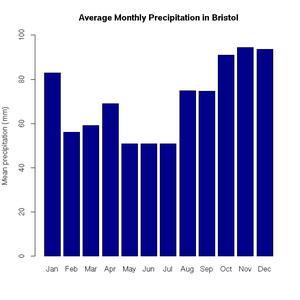
> bristol.precip <- c(82.9, 56.1, 59.2, 69, 50.8, 50.9, 50.8, 74.8, 74.7, 91.1, 94.5, 93.6)
> names(bristol.precip) <- c("Jan", "Feb", "Mar", "Apr", "May", "Jun", "Jul", "Aug", "Sep", "Oct", "Nov", "Dec")
> barplot(bristol.precip,
+ main="Average Monthly Precipitation in Bristol",
+ ylab="Mean precipitation (mm)",
+ ylim=c(0,100),
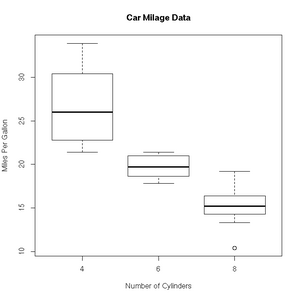
+ col=c("darkblue"))> boxplot(mpg~cyl,data=mtcars, main="Car Milage Data",
+ xlab="Number of Cylinders", ylab="Miles Per Gallon")> ?filled.countourData Structures
Packages
Examples of Common Tasks
Linear Regression
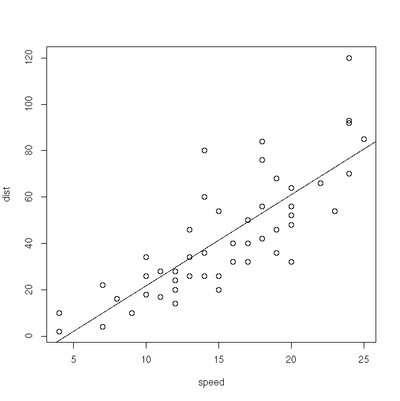
> plot(cars)
> res=lm(dist ~ speed, data=cars)
> abline(res)Exercise
- Weighted least squares. The lm function will accept a vector of weights, lm(... weights=...). If given, the function will optimise the line of best fit according a the equation of weighted least squares. Experiment with different linear model fits, given different weighting vectors. Some handy hints for creating a vector of weights:
- w1<-rep(0.1,50) will give you a vector, length 50, where each element has a value of 0.1. W1[1]<-10 will give the first element of the vector a value of 10.
- w2<-seq(from=0.02, to=1.0, by=0.02) provides a vector containing a sequence of values from 0.02 to 1.0 in steps of 0.02 (handily, again 50 in total).
Significance Testing
> boys_2=c(90.2, 91.4, 86.4, 87.6, 86.7, 88.1, 82.2, 83.8, 91, 87.4)
> girls_2=c(83.8, 86.2, 85.1, 88.6, 83, 88.9, 89.7, 81.3, 88.7, 88.4)
> res=var.test(boys_2,girls_2)
> res=t.test(boys_2, girls_2, var.equal=TRUE, paired=FALSE)