Difference between revisions of "Numerical Errors"
| Line 92: | Line 92: | ||
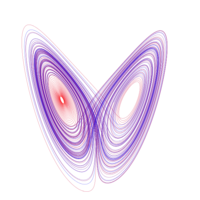
[[Image:600px-Lorenz_attractor.png|200px|thumb|right|The beautiful Lorenz attractor]] | [[Image:600px-Lorenz_attractor.png|200px|thumb|right|The beautiful Lorenz attractor]] | ||
| − | The equations | + | |
| + | In this example, we will take a look at the Lorenz attractor. The equations which govern it: | ||
| + | |||
: <math>\frac{dx}{dt} = \sigma (y - x)</math> | : <math>\frac{dx}{dt} = \sigma (y - x)</math> | ||
| Line 99: | Line 101: | ||
: <math>\frac{dz}{dt} = xy - \beta z</math> | : <math>\frac{dz}{dt} = xy - \beta z</math> | ||
| − | + | are deterministic, but also embody mathematical chaos. <math>\sigma</math> is called the '''Prandtl number''' and <math>\rho</math> is called the '''Rayleigh number'''. For this example, we have set: | |
* <math>\sigma</math> = 10 | * <math>\sigma</math> = 10 | ||
Revision as of 12:08, 7 January 2009
Unexpected things can happen when you use floating point numbers!
Introduction
Sooner or later, you're going to want to include real, aka floating-point, numbers in your programs. Beit for measured quantities, or parameterisations, but integers don't always cut it. Now this is all fine and as it should be. A word of warning, however. Programs containing floating point numbers can do very odd things indeed! Use them with care.
At core the reason that unexpected things happen is because you are sat in front of a digital computer, which is capable to storing and manipulating a finite number of discrete entities. This is contrasted against the infinite nature of real numbers. There are an inifinity of real numbers between o and 1, say, or indeed between 0.000001 and 0.0000011. Also there is no theoretical limit to the number of digits in a decimal fraction.
Digital computers must then approximate real numbers using a finite number of discrete ones, and it is this approximation which is the source of our surprises. Given the huge capacity of modern computers, it is easy to forget that this approximation. It's my goal in the sections below, to draw your attention to the areas in which ignoring this approximation will come back to bite you!
I didn't expect that!
Let's dive into our first example:
svn co http://source.ggy.bris.ac.uk/subversion-open/numerics/trunk ./numerics cd numerics/examples/example1 make
There are two programs in this directory, one written in C, the other in Fortran. Let's run the C program first:
./surprising_c.exe
This program does some very simple arithmetic and yet we start to see odd things happening already! For example the trigonometric function tan can give us hugely different values depending upon whether we give it a single precision- (typically stored using 4 bytes) or a double precision- (8 byte) number. To be fair [math]\displaystyle{ \tan(\pi/2) }[/math] (radians) is undefined, and so it's hard to say what the right output should be. However, is does highlight that you need to be vigilant when using floating-point numbers and not to expect that your program's behaviour will always be benign.
Less dramatic, but perhaps more alarming is the next section of the program. This time, we take three double-precision numbers, initialise them to some values and then add them together. So simple, what could go wrong? Lets! it turns out..
In this part of the program, we clearly see those approximations mentioned in the introduction. For example, we see that 0.43 is in fact stored as the approximation, 0.42999999999999999334. Then, when we factor in other approximations made in the intermeiate steps of summing up these numbers, we begin to understand that xx + (yy + zz) will indeed give us a different value to (xx + yy) + zz. Shocking!
The plain simplicity of these examples, coupled with their jarring results should warn us right away that there are many, many surprises waiting for us in programs involving floating-point numbers. Forewarned is forearmed.
Run the Fortran program (./surprising_f.exe) for completness and note that while the tan function may be better behaved, arithmetic is still not associative as a rule.
Algorithms Matter
In this example, we're going to compare two iterative routines:
cd ../example2
The two formulations, derived from Archimedes' method of exhaustion, diverge in their approximations to [math]\displaystyle{ \pi }[/math].
For both, [math]\displaystyle{ \pi \approx 6 \times 2^i \times t_i }[/math], where
[math]\displaystyle{ t_0 = \frac{1}{\sqrt{3}} }[/math]
For the first method,
[math]\displaystyle{ t_{i+1} = \frac{\sqrt{{t_i}^2 + 1} - 1}{t_i} }[/math]
The second method has,
[math]\displaystyle{ t_{i+1} = \frac{t_i}{\sqrt{{t_i}^2 + 1} +1} }[/math]
which you can see is mathematically equivalent, but differs in a subtle and important way - the subtraction of 1 in the numerator.
All very interesting, you say, but a bit dry. Let's just run the example:
make ./pi.exe
We see the values for the first and second methods as the iterations tick by:
ii first method second method sqrt(t_i**2 + 1.0)
0 3.46410155296326 3.46410155296326
1 3.21539025919465 3.21539025919465 1.03527617933213
2 3.15965989465839 3.15965989465840 1.00862896032215
3 3.14608616830022 3.14608616830024 1.00214567074349
4 3.14271455296452 3.14271455296452 1.00053569932786
5 3.14187300333673 3.14187300333646 1.00013388000792
...
23 3.14000715793035 3.14159260695893 1.00000000000000
24 3.22451494240339 3.14159260695892 1.00000000000000
25 2.79111747371586 3.14159260695892 1.00000000000000
The second method converges nicely, but the first method loses the way. What went wrong? The problem lies in the value of [math]\displaystyle{ \sqrt{{t_i}^2 + 1} }[/math]. We see that this gets closer and closer to 1.
In the first method we subtract 1 from a number very close to 1. The result? We lose a whole bunch of significant digits and so we lose information and hence accuracy. Since the value of [math]\displaystyle{ t_i }[/math] is used to compute the value of [math]\displaystyle{ t_{i+1} }[/math] this loss of accuracy is propagated to the next iteration and so on and so forth. It is not surprising, then, that the calculation becomes very inaccurate and does not converge upon an approximation to [math]\displaystyle{ \pi }[/math].
By contrast, we preserve the significant digits in the second method, keep good accuracy and so converge.
Deterministic, yes. Identical outputs? no
In this example, we will take a look at the Lorenz attractor. The equations which govern it:
- [math]\displaystyle{ \frac{dx}{dt} = \sigma (y - x) }[/math]
- [math]\displaystyle{ \frac{dy}{dt} = x (\rho - z) - y }[/math]
- [math]\displaystyle{ \frac{dz}{dt} = xy - \beta z }[/math]
are deterministic, but also embody mathematical chaos. [math]\displaystyle{ \sigma }[/math] is called the Prandtl number and [math]\displaystyle{ \rho }[/math] is called the Rayleigh number. For this example, we have set:
- [math]\displaystyle{ \sigma }[/math] = 10
- [math]\displaystyle{ \rho }[/math] = 28
- [math]\displaystyle{ \beta }[/math] = 8/3
cd ../example3 make test
gnuplot splot 'lorenz-noopt.dat' using 2:3:4 with lines replot 'lorenz-opt.dat' using 2:3:4 with lines